Flächeninhalt Raute (Rhombus) berechnen
Rechner und Formeln zur Berechnung des Flächeninhalts einer Raute
Raute Rechner
Raute (Rhombus)
Eine Raute hat 4 gleich lange Seiten und senkrecht stehende Diagonalen. Die Fläche berechnet sich aus den Diagonalen e und f.
Raute Visualisierung
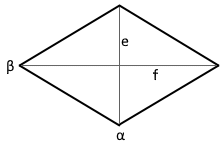
Das Diagramm zeigt eine Raute mit den Diagonalen e und f.
Die Diagonalen stehen senkrecht aufeinander und halbieren sich.
|
|
Was ist eine Raute (Rhombus)?
Eine Raute oder Rhombus ist ein spezielles Parallelogramm mit besonderen Eigenschaften:
- 4 gleiche Seiten: Alle Seitenlängen sind identisch
- Parallele Seiten: Gegenüberliegende Seiten sind parallel
- Gleiche Winkel: Gegenüberliegende Winkel sind gleich
- Senkrechte Diagonalen: Diagonalen stehen im rechten Winkel
- Halbierung: Diagonalen halbieren sich gegenseitig
- Flächenberechnung: A = (e × f) / 2
Eigenschaften der Raute
Die Raute hat charakteristische geometrische Eigenschaften:
Diagonalen
- Diagonalen stehen senkrecht aufeinander
- Diagonalen halbieren sich gegenseitig
- Diagonalen sind Symmetrieachsen der Raute
- Teilen die Raute in 4 kongruente rechtwinklige Dreiecke
Seiten und Winkel
- Alle vier Seiten sind gleich lang
- Gegenüberliegende Winkel sind gleich
- Benachbarte Winkel ergänzen sich zu 180°
- Winkelsumme beträgt 360°
Flächenberechnung verstehen
Die Flächenberechnung der Raute basiert auf den Diagonalen:
Das Grundprinzip
- Diagonale e: Erste Diagonale der Raute
- Diagonale f: Zweite Diagonale der Raute
- Formel: A = (e × f) / 2
- Diagonalen stehen senkrecht aufeinander!
Warum funktioniert das?
- Raute wird in 4 rechtwinklige Dreiecke geteilt
- Jedes Dreieck hat Fläche = (e/2 × f/2) / 2
- Gesamtfläche = 4 × (e × f) / 8 = (e × f) / 2
- Entspricht der Rechteckfläche der Diagonalen / 2
Anwendungen von Rauten
Rauten finden sich in vielen praktischen Bereichen:
Schmuck & Design
- Diamanten und Edelsteine
- Schmuckdesign und Ornamente
- Logo-Design und Corporate Identity
- Moderne Architektur-Elemente
Architektur & Bauwesen
- Fliesen und Bodenbeläge
- Fenster- und Fassadengestaltung
- Dachkonstruktionen
- Dekorative Bauelemente
Spiele & Unterhaltung
- Spielkarten (Karo-Symbol)
- Brettspiele und Puzzles
- Grafik-Design in Videospielen
- Muster und Ornamente
Wissenschaft & Technik
- Kristallstrukturen in Mineralien
- Molekulare Geometrie
- Optik und Lasertechnik
- Maschinenbau-Komponenten
Formeln für die Raute (Rhombus)
Flächeninhalt A
Halbes Produkt der beiden Diagonalen
Umfang P
Aus den Diagonalen über den Satz des Pythagoras
Seitenlänge a
Seitenlänge aus den Diagonalen berechnen
Winkel α
Spitzer Winkel der Raute
Winkel β
Stumpfer Winkel der Raute
Winkelbeziehung
Benachbarte Winkel ergänzen sich
Wichtige Hinweise
- e, f: Die beiden Diagonalen der Raute
- A: Flächeninhalt in Quadrateinheiten
- P: Umfang (4 × Seitenlänge)
- α, β: Die beiden verschiedenen Innenwinkel
- Diagonalen stehen senkrecht aufeinander
- Alle Seiten sind gleich lang
Rechenbeispiel für eine Raute
Gegeben
Gesucht: Alle Eigenschaften der Raute
1. Fläche berechnen
Halbes Produkt der Diagonalen
2. Seitenlänge berechnen
Pythagoras mit halben Diagonalen
3. Umfang berechnen
Viermal die Seitenlänge
4. Winkel berechnen
Komplementäre Winkel
5. Vollständige Raute
Eine klassische Raute mit dem Seitenverhältnis 4:3 der Diagonalen
Die Raute: Elegante Symmetrie in Geometrie und Design
Die Raute oder Rhombus ist eine der faszinierendsten geometrischen Formen, die mathematische Präzision mit ästhetischer Schönheit verbindet. Als spezielles Parallelogramm vereint sie die Eigenschaften gleicher Seitenlängen mit der Eleganz senkrecht stehender Diagonalen.
Mathematische Eleganz und Symmetrie
Die mathematischen Eigenschaften der Raute zeigen bemerkenswerte Eleganz:
- Perfekte Gleichseitigkeit: Alle vier Seiten sind exakt gleich lang
- Orthogonale Diagonalen: Die Diagonalen stehen im rechten Winkel zueinander
- Doppelte Symmetrie: Beide Diagonalen sind Spiegelachsen
- Punktsymmetrie: Symmetrisch zum Diagonalenschnittpunkt
- Einfache Flächenformel: A = (e × f) / 2 - elegant und praktisch
- Pythagoräische Beziehung: Seitenlänge folgt dem Satz des Pythagoras
Die Diagonalen als Schlüssel zum Verständnis
Die Diagonalen der Raute sind der Schlüssel zu allen ihren Eigenschaften:
Orthogonalität und Halbierung
Die Diagonalen stehen senkrecht aufeinander und halbieren sich gegenseitig. Dies teilt die Raute in vier kongruente rechtwinklige Dreiecke - die Basis für alle Berechnungen.
Flächenberechnung
Die Formel A = (e × f) / 2 entspricht der Hälfte des Rechtecks, das von den Diagonalen aufgespannt wird. Geometrisch elegant und rechnerisch einfach.
Seitenlängen-Beziehung
Jede Seite ist die Hypotenuse eines rechtwinkligen Dreiecks mit den Katheten e/2 und f/2. Daraus folgt: a = √((e/2)² + (f/2)²).
Winkelbeziehungen
Die Winkel lassen sich elegant über Arkustangens berechnen: α = 2·arctan(f/e). Benachbarte Winkel ergänzen sich immer zu 180°.
Kulturelle und praktische Bedeutung
Die Raute durchdringt Kultur und Technik auf vielfältige Weise:
- Heraldik und Symbolik: Diamant-Symbol für Wert und Beständigkeit
- Schmuckdesign: Klassische Form für Edelsteine und Ornamente
- Architektur: Strukturelle und ästhetische Elemente in Gebäuden
- Spielkarten: Das Karo-Symbol als universelles Zeichen
- Kristallographie: Rhombische Kristallsysteme in der Natur
- Grafik-Design: Moderne Logos und Corporate Identity
Verwandtschaft zu anderen geometrischen Formen
Die Raute steht in interessanten Beziehungen zu anderen Vierecken:
Quadrat als Spezialfall
Ein Quadrat ist eine Raute mit gleich langen Diagonalen (e = f) und 90°-Winkeln. Es ist die "perfekte" Raute mit maximaler Symmetrie.
Parallelogramm als Oberklasse
Jede Raute ist ein Parallelogramm, aber nicht jedes Parallelogramm ist eine Raute. Die Raute fügt die Bedingung gleicher Seitenlängen hinzu.
Drachenviereck-Verwandtschaft
Drachenvierecke haben ebenfalls senkrechte Diagonalen, aber unterschiedliche Seitenlängen. Die Raute ist ein spezielles symmetrisches Drachenviereck.
Rechteck-Dualität
Während Rechtecke rechte Winkel betonen, betont die Raute gleiche Seitenlängen. Beide sind spezielle Parallelogramme mit komplementären Eigenschaften.
Moderne Anwendungen und Innovationen
Die Raute inspiriert weiterhin moderne Entwicklungen:
- Nano-Technologie: Rhombische Gitterstrukturen in Materialwissenschaften
- Computer Graphics: Efziente Algorithmen für rhombische Pixelstrukturen
- Architektur: Moderne Fassadengestaltung mit rhombischen Elementen
- Spieleentwicklung: Isometrische Projektionen und Tile-basierte Welten
- Optik: Rhombische Prismen für Lichtbrechung und -lenkung
Zusammenfassung
Die Raute verkörpert geometrische Eleganz durch die Vereinigung von Gleichseitigkeit und orthogonalen Diagonalen. Ihre einfache Flächenformel A = (e × f) / 2 verbirgt eine reiche mathematische Struktur, die von der Pythagoräischen Beziehung bis zu trigonometrischen Winkelberechnungen reicht. Als Symbol für Perfektion und Wert durchdringt sie Kultur, Kunst und Technik. In einer Welt zunehmender geometrischer Komplexität bleibt die Raute ein zeitloses Beispiel dafür, wie mathematische Schönheit und praktische Anwendbarkeit Hand in Hand gehen können.
|
|
|
|