Kugel Rechner
Rechner und Formeln zur Berechnung von Oberfläche und Volumen einer Kugel
Kugel Rechner
Die perfekte Kugel
Die Kugel ist der perfekteste aller 3D-Körper mit vollständiger Symmetrie in alle Richtungen.
Kugel Eigenschaften
Die perfekte Kugel: Alle Punkte haben gleichen Abstand zum Mittelpunkt
Kugel Visualisierung
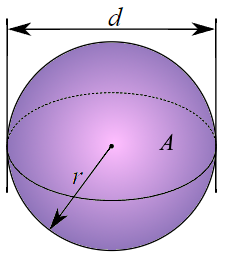
Die perfekte Kugel
Vollständige Symmetrie in allen Richtungen
Die Kugel ist der perfekteste aller geometrischen Körper.
Überall in der Natur zu finden.
|
|
Was ist eine Kugel?
Die Kugel ist der perfekteste aller dreidimensionalen geometrischen Körper:
- Definition: Alle Punkte haben gleichen Abstand zum Mittelpunkt
- Symmetrie: Vollständige Symmetrie in alle Richtungen
- Radius: Konstanter Abstand vom Zentrum zur Oberfläche
- Natur: Seifenblasen, Planeten, Atome
- Technik: Kugellager, Projektile, Behälter
- Mathematik: Elegante Formeln mit π
Geometrische Eigenschaften der Kugel
Die Kugel zeigt einzigartige geometrische Eigenschaften:
Grundparameter
- Radius r: Abstand vom Mittelpunkt zur Oberfläche
- Durchmesser d: Doppelter Radius (d = 2r)
- Umfang P: Umfang des größten Kreises
- Mittelpunkt: Symmetriezentrum der Kugel
Besondere Eigenschaften
- Vollsymmetrie: Symmetrisch in alle Richtungen
- Minimale Oberfläche: Kleinste Oberfläche für gegebenes Volumen
- Maximales Volumen: Größtes Volumen für gegebene Oberfläche
- Perfekte Rundung: Keine Kanten oder Ecken
Mathematische Beziehungen der Kugel
Die Kugel folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen wächst kubisch mit dem Radius. Elegante Formel mit π.
Oberflächen-Formel
Die Oberfläche wächst quadratisch mit dem Radius. Vier mal die Kreisfläche.
Anwendungen der Kugel
Kugeln finden Anwendung in verschiedenen Bereichen:
Natur & Physik
- Seifenblasen (Oberflächenminimierung)
- Wassertropfen (Oberflächenspannung)
- Planeten und Sterne
- Atomkerne und Moleküle
Technik & Ingenieurswesen
- Kugellager (reibungsarm)
- Druckbehälter (optimal)
- Projektile (aerodynamisch)
- Kugelventile
Sport & Freizeit
- Fußbälle, Basketbälle
- Tischtennisbälle
- Billardkugeln
- Golfbälle (aerodynamisch)
Mathematik & Geometrie
- Geometrische Grundform
- Symmetriebeispiel
- Optimierungsprobleme
- π-Berechnungen
Formeln zur Berechnung einer Kugel
Radius (r)
Radius aus Umfang berechnen
Durchmesser (d)
Durchmesser ist doppelter Radius
Umfang (P)
Umfang des größten Kreises
Oberfläche (S)
Vier mal die Kreisfläche
Schnittfläche (A)
Kreisfläche durch den Mittelpunkt
Volumen (V)
Das klassische 4/3 π r³
Berechnungsbeispiel für eine Kugel
Gegeben
Gesucht: Alle Parameter der Kugel
1. Durchmesser-Berechnung
Für r = 10 cm:
\[d = 2 \cdot r = 2 \cdot 10\] \[d = 20 \text{ cm}\]Der Durchmesser beträgt 20 cm
2. Umfang-Berechnung
Mit r = 10 cm:
\[P = 2 \cdot π \cdot r = 2 \cdot π \cdot 10\] \[P = 20π ≈ 62.83 \text{ cm}\]Der Umfang beträgt etwa 62.83 cm
3. Oberflächen-Berechnung
Mit r = 10 cm:
\[S = 4 \cdot π \cdot r^2 = 4 \cdot π \cdot 10^2\] \[S = 4 \cdot π \cdot 100 = 400π\] \[S ≈ 1256.64 \text{ cm}^2\]Die Oberfläche beträgt etwa 1256.64 cm²
4. Volumen-Berechnung
Mit r = 10 cm:
\[V = \frac{4}{3} \cdot π \cdot r^3 = \frac{4}{3} \cdot π \cdot 10^3\] \[V = \frac{4}{3} \cdot π \cdot 1000 = \frac{4000π}{3}\] \[V ≈ 4188.79 \text{ cm}^3\]Das Volumen beträgt etwa 4188.79 cm³
5. Schnittflächen-Berechnung
Mit r = 10 cm:
\[A = π \cdot r^2 = π \cdot 10^2\] \[A = π \cdot 100 = 100π\] \[A ≈ 314.16 \text{ cm}^2\]Die Schnittfläche beträgt etwa 314.16 cm²
6. Zusammenfassung
Die perfekte Kugel mit Radius 10 cm
Die Kugel: Perfektion der Geometrie und Natur
Die Kugel ist der perfekteste aller geometrischen Körper und verkörpert die absolute Symmetrie und Harmonie. Als einziger dreidimensionaler Körper, bei dem alle Punkte der Oberfläche den gleichen Abstand zum Mittelpunkt haben, zeigt sie mathematische Eleganz und praktische Perfektion. In der Natur entstehen Kugeln überall dort, wo die Natur nach Energieminimierung strebt - von Seifenblasen bis zu Planeten.
Die Geometrie der Perfektion
Die Kugel zeigt die ultimative geometrische Vollkommenheit:
- Vollständige Symmetrie: Symmetrisch bezüglich jeder Ebene durch den Mittelpunkt
- Konstanter Radius: Alle Oberflächenpunkte haben gleichen Abstand zum Zentrum
- Minimale Oberfläche: Kleinste Oberfläche für gegebenes Volumen
- Maximales Volumen: Größtes Volumen für gegebene Oberfläche
- Keine Kanten: Perfekt runde Form ohne Ecken oder Kanten
- Optimale Form: Grundlage für viele Optimierungsprobleme
- Universelle Anwendung: Von Atomen bis zu Galaxien
Mathematische Eleganz
Formel-Einfachheit
Die Kugel-Formeln sind elegant und einprägsam: 4πr² für die Oberfläche und 4/3πr³ für das Volumen - klassische mathematische Schönheit.
Symmetrie-Perfektion
Als einziger Körper mit vollständiger Rotations- und Spiegelsymmetrie ist die Kugel das Ideal der geometrischen Perfektion.
Natürliche Entstehung
Überall wo die Natur Energie minimiert - Seifenblasen, Wassertropfen, Planeten - entstehen kugelförmige Strukturen.
Technische Optimierung
In der Technik nutzt man kugelförmige Designs für minimale Reibung (Kugellager) und optimale Druckverteilung (Druckbehälter).
Zusammenfassung
Die Kugel verkörpert die absolute Perfektion in der Geometrie. Als einziger dreidimensionaler Körper mit vollständiger Symmetrie in alle Richtungen zeigt sie die Eleganz mathematischer Gesetze und die Weisheit der Natur. Ihre einfachen, aber mächtigen Formeln mit π beschreiben präzise alle geometrischen Eigenschaften. Von der Entstehung von Seifenblasen durch Oberflächenminimierung über die Kugelgestalt von Planeten durch Gravitation bis hin zu technischen Anwendungen in Kugellagern und Druckbehältern - die Kugel ist überall dort zu finden, wo die Natur oder der Mensch nach Perfektion streben. Sie verbindet mathematische Schönheit mit praktischem Nutzen und bleibt der ultimative geometrische Körper für Optimierung und Effizienz.
|
|
|
|