Kugelschicht Rechner
Onlinerechner und Formeln zur Berechnung der Parameter einer Kugelschicht
Kugelschicht Rechner
Die Kugelschicht
Die Kugelschicht ist ein Teil einer Kugel, der von zwei parallelen Ebenen ausgeschnitten wird.
Kugelschicht Eigenschaften
Die Kugelschicht: Segment zwischen zwei parallelen Ebenen
Kugelschicht Visualisierung
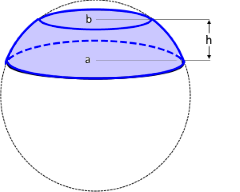
Die Kugelschicht
Segment zwischen zwei parallelen Ebenen
Komplexe Geometrie mit gekrümmter Zone.
Präzise Schnittführung durch Parallelebenen.
|
|
Was ist eine Kugelschicht?
Die Kugelschicht ist ein spezieller geometrischer Körper:
- Definition: Teil einer Kugel zwischen zwei parallelen Ebenen
- Kugelzone: Der gekrümmte Flächenteil der Schicht
- Schnittkreise: Kreisförmige Ränder mit Radien a und b
- Höhe h: Abstand zwischen den beiden Schnittebenen
- Anwendung: Architektur, Ingenieurswesen, Astronomie
- Besonderheit: Komplexe Berechnungsformeln durch Geometrie
Geometrische Eigenschaften der Kugelschicht
Die Kugelschicht zeigt komplexe geometrische Eigenschaften:
Grundparameter
- Radius a: Radius des oberen Schnittkreises
- Radius b: Radius des unteren Schnittkreises
- Höhe h: Abstand zwischen den parallelen Ebenen
- Kugelradius r: Radius der ursprünglichen Kugel
Besondere Eigenschaften
- Kugelzone: Gekrümmte Mantelfläche zwischen den Kreisen
- Variable Radien: a und b können unterschiedlich groß sein
- Komplexe Formeln: Aufwendige Berechnungen durch Geometrie
- Positionsabhängig: Lage in der ursprünglichen Kugel relevant
Mathematische Beziehungen der Kugelschicht
Die Kugelschicht folgt komplexen mathematischen Gesetzen:
Volumen-Formel
Das Volumen berücksichtigt beide Radien und die Höhe. Komplexe Abhängigkeiten durch Schnittgeometrie.
Oberflächen-Formel
Die Oberfläche umfasst Mantel- und Kreisflächen. Abhängig vom Kugelradius r.
Anwendungen der Kugelschicht
Kugelschichten finden Anwendung in verschiedenen Bereichen:
Architektur & Bau
- Kuppel-Segmente
- Gewölbeberechnungen
- Moderne Architektur
- Brückenkonstruktionen
Geodäsie & Astronomie
- Erdschicht-Modellierung
- Planeten-Segmente
- Atmosphären-Schichten
- Himmelskugel-Bereiche
Ingenieurswesen
- Behälter-Segmente
- Rohrleitungssysteme
- Maschinenbau
- Strömungstechnik
Wissenschaft & Forschung
- Physikalische Modelle
- Materialwissenschaft
- Biomechanik
- Kristallographie
Formeln zur Kugelschicht
Radius der Kugel (r)
Komplexe Berechnung aus den Schnittparametern
Mantelfläche (M)
Gekrümmte Oberfläche der Kugelzone
Oberfläche der Kugelschicht (S)
Mantelfläche plus beide Kreisflächen
Volumen der Kugelschicht (V)
Volumen zwischen den parallelen Ebenen
Abstand zum oberen Rand (dt)
Position der Schicht in der Kugel
Abstand zur Kugelmitte (dm)
Mittlere Position der Schicht
Berechnungsbeispiel für eine Kugelschicht
Gegeben
Gesucht: Alle Parameter der Kugelschicht
1. Kugelradius-Berechnung
Für a = 6, b = 4, h = 2:
\[\frac{a^2 - b^2 - h^2}{2h} = \frac{36 - 16 - 4}{4} = 4\] \[r = \sqrt{36 + 16} = \sqrt{52} ≈ 7.21 \text{ cm}\]Der Kugelradius beträgt etwa 7.21 cm
2. Mantelflächen-Berechnung
Mit r ≈ 7.21 cm, h = 2 cm:
\[M = 2 \cdot π \cdot r \cdot h\] \[M = 2 \cdot π \cdot 7.21 \cdot 2\] \[M ≈ 90.63 \text{ cm}^2\]Die Mantelfläche beträgt etwa 90.63 cm²
3. Gesamtoberflächen-Berechnung
Mit den berechneten Werten:
\[S = π \cdot (2rh + a^2 + b^2)\] \[S = π \cdot (28.84 + 36 + 16)\] \[S = π \cdot 80.84 ≈ 254.02 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 254.02 cm²
4. Volumen-Berechnung
Mit a = 6, b = 4, h = 2:
\[V = \frac{πh}{6} \cdot (3a^2 + 3b^2 + h^2)\] \[V = \frac{2π}{6} \cdot (108 + 48 + 4)\] \[V = \frac{π}{3} \cdot 160 ≈ 167.55 \text{ cm}^3\]Das Volumen beträgt etwa 167.55 cm³
5. Positionsbestimmung
Abstände in der Kugel:
\[d_t = d_m = \frac{36 - 16 - 4}{4} = 4 \text{ cm}\]Abstand zur Kugelmitte: 4 cm
Die Schicht liegt 4 cm von der Kugelmitte entfernt
6. Zusammenfassung
Die Kugelschicht mit a=6, b=4, h=2
7. Geometrische Analyse
a/b = 6/4 = 1.5
h/r = 2/7.21 ≈ 0.28
Außerhalb Zentrum
Konvexe Form
Die Schicht liegt außerhalb der Kugelmitte mit konvexer Krümmung
Die Kugelschicht: Komplexe Geometrie zwischen parallelen Ebenen
Die Kugelschicht ist ein faszinierender geometrischer Körper, der die Komplexität dreidimensionaler Schnittgeometrie eindrucksvoll demonstriert. Als Teil einer Kugel, der von zwei parallelen Ebenen ausgeschnitten wird, vereint sie gekrümmte und ebene Flächenelemente zu einer einzigartigen Form. Die mathematische Herausforderung liegt in den komplexen Berechnungsformeln, die die Position, Orientierung und Größe der Schicht in der ursprünglichen Kugel berücksichtigen müssen. Die Kugelschicht zeigt, wie aus einfachen Schnitten komplexe geometrische Beziehungen entstehen.
Die Geometrie der Parallelschnitte
Die Kugelschicht zeigt die Faszination geometrischer Schnittoperationen:
- Parallele Ebenen: Zwei parallele Schnittebenen definieren die Schicht
- Variable Radien: Schnittkreise mit unterschiedlichen Radien a und b
- Kugelzone: Die gekrümmte Mantelfläche zwischen den Kreisen
- Komplexe Positionierung: Lage in der ursprünglichen Kugel entscheidend
- Höhenabhängigkeit: Schichthöhe h bestimmt alle Eigenschaften mit
- Geometrische Rekonstruktion: Kugelradius aus Schichtparametern berechenbar
- Vielfältige Anwendungen: Von Architektur bis Astronomie
Mathematische Komplexität
Rekonstruktions-Formeln
Die Berechnung des ursprünglichen Kugelradius aus den Schichtparametern zeigt die mathematische Eleganz der inversen Geometrie.
Positions-Mathematik
Die Abstandsformeln ermöglichen die präzise Lokalisierung der Schicht innerhalb der ursprünglichen Kugel.
Praktische Relevanz
In Architektur und Ingenieurswesen ermöglichen Kugelschichten präzise Berechnungen von Kuppel-Segmenten und gewölbten Strukturen.
Wissenschaftliche Anwendung
In Geodäsie und Astronomie helfen Kugelschichten bei der Modellierung von Erdschichten und Atmosphären-Segmenten.
Zusammenfassung
Die Kugelschicht verkörpert die Komplexität und Eleganz geometrischer Schnittoperationen. Als Teil einer Kugel zwischen zwei parallelen Ebenen zeigt sie, wie aus einfachen Schnitten hochkomplexe mathematische Beziehungen entstehen. Ihre Formeln - von der Rekonstruktion des ursprünglichen Kugelradius über die Positions-bestimmung bis hin zu Volumen- und Oberflächenberechnungen - demonstrieren die Macht der analytischen Geometrie. Von architektonischen Kuppel-Segmenten über geodätische Erdschicht- Modellierungen bis hin zu astronomischen Anwendungen zeigt die Kugelschicht ihre universelle Bedeutung. Sie verbindet die Reinheit geometrischer Schnitte mit der praktischen Notwendigkeit komplexer Berechnungen und bleibt ein fundamentales Beispiel für die Schönheit mathematischer Geometrie in drei Dimensionen.
|
|
|
|