Kugelkeil Rechner
Rechner und Formeln zur Berechnung eines Kugelkeils
Kugelkeil Rechner
Der Kugelkeil
Der Kugelkeil ist ein winkelförmiger Ausschnitt aus einer Vollkugel, entstanden durch zwei Halbebenen.
Kugelkeil Eigenschaften
Der Kugelkeil: Winkelabhängiger Ausschnitt aus einer Vollkugel
Kugelkeil Visualisierung
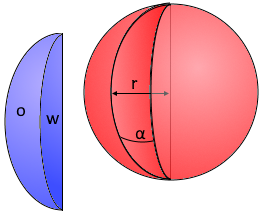
Der Kugelkeil
Winkelförmiger Ausschnitt aus einer Vollkugel
Der Kugelkeil mit variablem Winkel.
Von zwei Halbebenen begrenzt.
|
|
Was ist ein Kugelkeil?
Der Kugelkeil ist ein spezieller geometrischer Körper:
- Definition: Teil einer Vollkugel zwischen zwei Halbebenen
- Begrenzung: Zwei Halbebenen mit gemeinsamem Durchmesser
- Oberfläche: Kugelzweieck plus zwei Halbkreise
- Winkel: Bestimmt die Größe des Ausschnitts
- Anwendung: Geometrie, Architektur, Mathematik
- Besonderheit: Winkelproportionale Eigenschaften
Geometrische Eigenschaften des Kugelkeils
Der Kugelkeil zeigt winkelabhängige geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der ursprünglichen Kugel
- Winkel α: Öffnungswinkel zwischen den Halbebenen
- Halbebenen: Zwei begrenzende Flächen durch den Mittelpunkt
- Kugelzweieck: Gekrümmte Randfläche auf der Kugel
Besondere Eigenschaften
- Winkelproportionalität: Alle Eigenschaften proportional zu α
- Symmetrie: Spiegelsymmetrisch zur Winkelhalbierenden
- Vollständigkeit: Bei α = 360° ergibt sich die Vollkugel
- Keilfläche: Immer π × r² unabhängig vom Winkel
Mathematische Beziehungen des Kugelkeils
Der Kugelkeil folgt winkelabhängigen mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist direkt proportional zum Winkel α. Winkel in Bogenmaß (Radiant) einsetzen.
Randflächen-Formel
Die Randfläche (Kugelzweieck) proportional zu α. Gekrümmte Oberfläche auf der Kugel.
Anwendungen des Kugelkeils
Kugelkeile finden Anwendung in verschiedenen Bereichen:
Geodäsie & Kartographie
- Zeitzonen-Berechnung
- Längengrade und Sektoren
- Erdkugel-Aufteilung
- Geografische Koordinaten
Astronomie & Navigation
- Himmelskugel-Sektoren
- Stern-Koordinatensysteme
- Satellitennavigation
- Planetenbeobachtung
Architektur & Design
- Kuppel-Segmente
- Runde Gebäudeteile
- Skulpturale Elemente
- Industriedesign
Mathematik & Physik
- Integralrechnung
- Volumenberechnung
- Wahrscheinlichkeitsrechnung
- Geometrische Studien
Formeln zum Kugelkeil
Volumen (V)
Winkel α in Bogenmaß (Radiant)
Randfläche (O)
Kugelzweieck - gekrümmte Oberfläche
Keilfläche (W)
Konstant - unabhängig vom Winkel
Gesamte Oberfläche (S)
Summe aus Rand- und Keilfläche
Winkelumrechnung
\(α_{rad} = α_{grad} \cdot \frac{π}{180°}\)
\(α_{grad} = α_{rad} \cdot \frac{180°}{π}\)
\(360° = 2π \text{ rad}\)
Wichtig: Für Berechnungen muss α in Radiant vorliegen
Berechnungsbeispiel für einen Kugelkeil
Gegeben
Gesucht: Alle Parameter des Kugelkeils
1. Winkel-Umrechnung
Umrechnung von Grad in Radiant:
\[α = 60° \cdot \frac{π}{180°} = \frac{π}{3}\] \[α = \frac{π}{3} ≈ 1.047 \text{ rad}\]Der Winkel beträgt π/3 Radiant
2. Volumen-Berechnung
Mit α = π/3 und r = 6:
\[V = \frac{π}{3} \cdot \frac{2}{3} \cdot 6^3\] \[V = \frac{π}{3} \cdot \frac{2}{3} \cdot 216 = \frac{144π}{9} = 48π\] \[V ≈ 150.80 \text{ cm}^3\]Das Volumen beträgt etwa 150.80 cm³
3. Randflächen-Berechnung
Mit α = π/3 und r = 6:
\[O = 2 \cdot \frac{π}{3} \cdot 6^2\] \[O = 2 \cdot \frac{π}{3} \cdot 36 = \frac{72π}{3} = 24π\] \[O ≈ 75.40 \text{ cm}^2\]Die Randfläche beträgt etwa 75.40 cm²
4. Keilflächen-Berechnung
Mit r = 6 (unabhängig vom Winkel):
\[W = π \cdot r^2 = π \cdot 6^2\] \[W = π \cdot 36 = 36π\] \[W ≈ 113.10 \text{ cm}^2\]Die Keilfläche beträgt etwa 113.10 cm²
5. Gesamtoberfläche
Summe aus Rand- und Keilfläche:
\[S = O + W = 24π + 36π = 60π\] \[S ≈ 188.50 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 188.50 cm²
6. Zusammenfassung
Der Kugelkeil mit 60° Öffnungswinkel
7. Anteil an der Vollkugel
V = 150.80 cm³
V = 904.78 cm³
60°/360° = 1/6
Der 60°-Kugelkeil hat 1/6 des Volumens der Vollkugel
Der Kugelkeil: Winkelgeometrie der Kugel
Der Kugelkeil ist ein faszinierender geometrischer Körper, der die Eleganz der Kugelgeometrie mit der Präzision winkelbasierter Berechnungen verbindet. Als winkelförmiger Ausschnitt aus einer Vollkugel, begrenzt von zwei Halbebenen durch den Mittelpunkt, zeigt er die perfekte Proportionalität zwischen Winkel und geometrischen Eigenschaften. Der Kugelkeil verkörpert die mathematische Schönheit winkelabhängiger Geometrie und findet breite Anwendung in Geodäsie, Astronomie und Architektur.
Die Geometrie des Winkels
Der Kugelkeil zeigt die Faszination winkelabhängiger Geometrie:
- Halbebenen-Begrenzung: Zwei Halbebenen durch einen gemeinsamen Durchmesser
- Kugelzweieck: Gekrümmte Randfläche auf der ursprünglichen Kugeloberfläche
- Winkelproportionalität: Volumen und Randfläche direkt proportional zum Winkel
- Konstante Keilfläche: π × r² unabhängig vom Öffnungswinkel
- Symmetrie: Spiegelsymmetrisch zur Winkelhalbierenden
- Skalierbarkeit: Von 0° bis 360° kontinuierlich definiert
- Universelle Anwendung: Von Zeitzonen bis zu Himmelskugel-Sektoren
Mathematische Eleganz
Proportionalitäts-Gesetze
Die elegante Proportionalität zwischen Winkel und Volumen (α × 2/3 × r³) sowie Randfläche (2α × r²) zeigt die mathematische Reinheit des Kugelkeils.
Winkel-Geometrie
Die Verwendung von Bogenmaß (Radiant) ermöglicht direkte Proportionalität und elegante Formeln ohne komplizierte Umrechnungsfaktoren.
Praktische Relevanz
Von Zeitzonen-Berechnungen über astronomische Koordinaten bis zu architektonischen Kuppel-Segmenten - der Kugelkeil ist überall präsent.
Geodätische Bedeutung
In der Geodäsie ermöglicht der Kugelkeil präzise Berechnungen von Erdkugel-Sektoren, Längengraden und geografischen Koordinaten.
Zusammenfassung
Der Kugelkeil verkörpert die perfekte Harmonie zwischen Winkelgeometrie und Kugelvolumen. Als winkelförmiger Ausschnitt aus einer Vollkugel zeigt er die elegante Proportionalität mathematischer Gesetze - Volumen und Randfläche sind direkt proportional zum Öffnungswinkel, während die Keilfläche konstant bleibt. Diese mathematische Klarheit macht ihn zu einem unverzichtbaren Werkzeug in Geodäsie, Astronomie und Navigation. Von der Aufteilung der Erdkugel in Zeitzonen über die Berechnung von Himmelskugel-Sektoren bis hin zu architektonischen Anwendungen in Kuppelbauten - der Kugelkeil verbindet theoretische Winkelgeometrie mit praktischen Lösungen. Er demonstriert eindrucksvoll, wie einfache geometrische Prinzipien zu mächtigen mathematischen Werkzeugen werden, die unsere Welt von der kleinsten Winkelmessung bis zur größten geodätischen Berechnung prägen.
|
|
|
|