Rotationsellipsoid Rechner
Rechner und Formeln zur Berechnung von Volumen und Oberfläche eines Rotationsellipsoids
Ellipsoid Rechner
Das Rotationsellipsoid
Das Rotationsellipsoid ist ein Spheroid entstanden durch Rotation einer Ellipse um eine Achse.
Rotationsellipsoid Eigenschaften
Der Spheroid: Entstanden durch Ellipsen-Rotation
Ellipsoid Typen
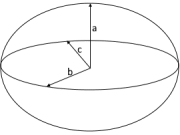
Abgeplattetes (oblates) Ellipsoid
a < b - Linsenform wie die Erde
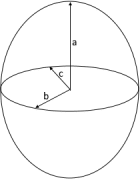
Verlängertes (prolates) Ellipsoid
a > b - Rugby-Ball Form
Rotationsellipsoide in der Natur.
Von Planeten bis zu Molekülen.
|
|
Was ist ein Rotationsellipsoid?
Das Rotationsellipsoid (Spheroid) ist ein fundamentaler geometrischer Körper:
- Definition: Entstanden durch Rotation einer Ellipse um eine Achse
- Typen: Oblate (abgeplattet) und prolate (verlängert)
- Eigenschaften: Rotationssymmetrisch um eine Achse
- Natur: Erdform, Planetenformen
- Technik: Behälter, aerodynamische Körper
- Mathematik: Elegante Formeln mit π und Quadratwurzeln
Geometrische Eigenschaften des Rotationsellipsoids
Das Rotationsellipsoid zeigt faszinierende geometrische Eigenschaften:
Grundparameter
- Halbachsen: a (Rotationsachse), b (Äquatorial)
- Meridianellipse: Schnitt durch Rotationsachse
- Parallelkreise: Kreisförmige Querschnitte
- Rotationssymmetrie: Unendlich viele Spiegelachsen
Besondere Eigenschaften
- Exzentrität: Maß für Abweichung von Kugelform
- Abplattung: f = (a-b)/a bei oblaten Ellipsoiden
- Krümmung: Variiert über die Oberfläche
- Geodäsie: Grundlage für Erdvermessung
Mathematische Beziehungen
Das Rotationsellipsoid folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Gleiche Formel für oblate und prolate Formen. Elegant und einfach.
Oberflächen-Formel
Unterschiedliche Formeln für oblate/prolate. Mit arcsin/arcsinh Funktionen.
Anwendungen des Rotationsellipsoids
Rotationsellipsoide finden Anwendung in verschiedenen Bereichen:
Geodäsie & Kartographie
- Erdmodellierung (WGS84, GRS80)
- GPS-Koordinatensysteme
- Kartenprojektion
- Satellitenbahnen
Astronomie & Astrophysik
- Planetenformen
- Asteroidenmodellierung
- Stellare Objekte
- Gravitationsfelder
Ingenieurswesen
- Behälterdesign
- Drucktanks
- Aerodynamische Körper
- Optische Linsen
Physik & Chemie
- Atomkerne
- Molekülgeometrie
- Kristallstrukturen
- Quantenmechanik
Formeln zum Rotationsellipsoid
Volumen (V)
Universelle Formel für alle Rotationsellipsoide
Oberfläche (S) - Oblat
Für abgeplattete Ellipsoide (a < b)
Oberfläche (S) - Prolat
Für verlängerte Ellipsoide (a > b)
Kugel (Spezialfall)
Wenn a = b (perfekte Kugel)
Ellipsoid Parameter
\(e = \sqrt{1-\frac{b^2}{a^2}}\)
\(f = \frac{a-b}{a}\)
\(\frac{b}{a}\)
Oblat/Prolat
Alle Parameter folgen aus den Halbachsen a und b
Berechnungsbeispiel für ein Rotationsellipsoid
Gegeben
Gesucht: Volumen und Oberfläche des verlängerten Ellipsoids
1. Volumen-Berechnung
Für a = 6, b = 4:
\[V = \frac{4}{3} \cdot \pi \cdot 6 \cdot 4^2\] \[V = \frac{4}{3} \cdot \pi \cdot 6 \cdot 16\] \[V = \frac{4}{3} \cdot \pi \cdot 96 = 128\pi\] \[V ≈ 402.12 \text{ cm}^3\]Das Volumen beträgt etwa 402.12 cm³
2. Oberflächen-Berechnung (Prolat)
Da a > b (6 > 4):
\[\sqrt{a^2-b^2} = \sqrt{36-16} = \sqrt{20} = 2\sqrt{5}\] \[\arcsin\left(\frac{2\sqrt{5}}{6}\right) ≈ 0.7297\] \[S = 2\pi \cdot 16 + \frac{2\pi \cdot 6 \cdot 16}{2\sqrt{5}} \cdot 0.7297\] \[S ≈ 271.77 \text{ cm}^2\]Die Oberfläche beträgt etwa 271.77 cm²
3. Ellipsoid-Parameter
Zusätzliche Parameter:
\[e = \sqrt{1-\frac{16}{36}} = \sqrt{\frac{5}{9}} ≈ 0.745\] \[f = \frac{6-4}{6} = \frac{1}{3} ≈ 0.333\] \[\frac{b}{a} = \frac{4}{6} = \frac{2}{3} ≈ 0.667\]Exzentrität, Abplattung und Achsenverhältnis
4. Das verlängerte Ellipsoid
Das verlängerte Rotationsellipsoid (Rugby-Ball Form)
Das Rotationsellipsoid: Perfektion der Natur und Mathematik
Das Rotationsellipsoid ist ein faszinierender geometrischer Körper, der die Eleganz der Natur und die Präzision der Mathematik vereint. Entstanden durch die Rotation einer Ellipse um eine ihrer Hauptachsen, bildet es die Grundlage für die Beschreibung der Erdform und unzähliger anderer Objekte in Natur und Technik. Die mathematische Schönheit liegt in den eleganten Formeln mit π, Quadratwurzeln und trigonometrischen Funktionen, die alle geometrischen Eigenschaften perfekt beschreiben.
Die Geometrie der Rotation
Das Rotationsellipsoid zeigt die Perfektion der rotationssymmetrischen Geometrie:
- Meridianellipse: Jeder Schnitt durch die Rotationsachse ist eine Ellipse
- Parallelkreise: Alle Querschnitte sind perfekte Kreise
- Rotationssymmetrie: Unendlich viele Spiegelebenen durch die Achse
- Zwei Grundtypen: Oblate (abgeplattet) und prolate (verlängert) Formen
- Spezialfall Kugel: Wenn beide Halbachsen gleich sind
- Geodätische Bedeutung: Grundlage für die Erdvermessung
- Universelle Anwendung: Von Atomkernen bis zu Galaxien
Mathematische Eleganz
Formel-Perfektion
Die Volumenformel ist universell gültig, während die Oberflächenformeln für oblate und prolate Formen die Schönheit der Integral- und Differentialrechnung zeigen.
Geodätische Präzision
Als Grundlage für GPS und Kartographie ermöglicht das Rotationsellipsoid präzise Navigation und Vermessung auf der Erde.
Natürliche Perfektion
Von der Erdform über Planetengestalten bis zu molekularen Strukturen - das Rotationsellipsoid ist überall in der Natur zu finden.
Technische Vollendung
In Ingenieurswesen und Design bietet das Rotationsellipsoid optimale Lösungen für Behälter, aerodynamische Körper und optische Systeme.
Zusammenfassung
Das Rotationsellipsoid verkörpert die perfekte Harmonie zwischen mathematischer Eleganz und praktischer Anwendung. Seine durch Ellipsenrotation entstehende Form, beschrieben durch elegante Formeln mit π und Quadratwurzeln, macht es zu einem fundamentalen Baustein der Geometrie. Von der präzisen Beschreibung der Erdgestalt in der Geodäsie über astronomische Anwendungen bis hin zu ingenieurtechnischen Lösungen - das Rotationsellipsoid verbindet theoretische Schönheit mit praktischem Nutzen. Als Spheroid zeigt es, wie die Rotation einer einfachen Ellipse zu einem der wichtigsten geometrischen Körper der Wissenschaft und Technik führt, der unsere Welt von der kleinsten molekularen bis zur größten planetaren Skala prägt.
|
|
|
|