Torus Calculator
Calculator and formulas for calculating a torus
Torus Calculator
The Torus
The torus is a donut-shaped ring form with hole.
Torus Properties
The torus: Classic donut with characteristic hole
Torus Visualization
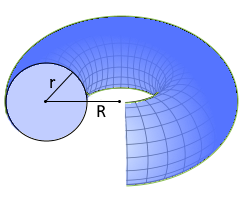
Torus Cross Section
Shows the characteristic donut shape
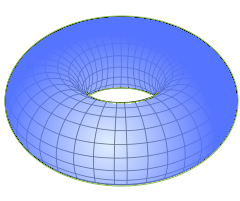
Torus 3D View
Complete three-dimensional form
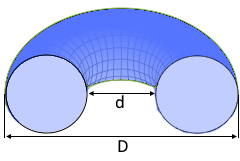
Torus Diameter
Major and minor diameters
Classic donut with through hole.
Solid of revolution around central axis.
|
|
What is a torus?
The torus is a fundamental geometric form:
- Definition: Solid of revolution created by rotating a circle around an axis
- Shape: Donut or life ring shape with characteristic through hole
- Parameters: Major radius R (center to tube center) and minor radius r (tube radius)
- Condition: R > r for classic torus with hole
- Diameters: Major diameter D = 2(R+r), minor diameter d = 2(R-r)
- Application: Architecture, mechanical engineering, mathematics, design
Geometric properties of the torus
The torus shows characteristic geometric properties:
Basic parameters
- Major radius R: Distance from torus center to tube center
- Minor radius r: Radius of the rotating tube
- Major diameter D: D = 2(R+r) - outer diameter
- Minor diameter d: d = 2(R-r) - hole diameter
Special properties
- Through hole: Characteristic hole in the center
- Rotational symmetry: Symmetric around the central axis
- Donut shape: Classic bulging ring form
- Smooth surface: No edges or corners
Mathematical relationships of the torus
The torus follows elegant mathematical laws:
Volume formula
The volume is proportional to R and r². Elegantly characterized by π².
Surface area formula
The surface area is proportional to R and r. Simple linear relationship to both radii.
Applications of the torus
Tori find applications in various fields:
Architecture & Construction
- Modern building architecture
- Dome and roof constructions
- Bridge elements
- Sculptural structures
Mechanical Engineering & Technology
- Sealing rings (O-rings)
- Tires and tubes
- Piping systems
- Machine parts
Science & Research
- Plasma physics (Tokamak reactors)
- Topology and mathematics
- Fluid mechanics
- Materials science
Design & Art
- Jewelry design
- Sculptural artworks
- Product design
- Furniture design
Formulas for the torus
Volume (V)
Volume of torus with characteristic π² factor
Surface Area (S)
Total surface area of the torus
Major Diameter (D)
Outer diameter of the torus
Minor Diameter (d)
Diameter of the central hole
Minor Radius (r)
Tube radius from diameters
Major Radius (R)
Main radius from diameter and tube radius
Torus Parametrization
Parametric representation with u ∈ [0,2π] and v ∈ [0,2π]. These equations describe every point on the torus surface.
Calculation examples for a torus
Example 1: Input with radii
Find: All parameters of the torus
1. Diameter calculation
For R = 8 cm, r = 3 cm:
\[D = 2(R + r) = 2(8 + 3) = 22 \text{ cm}\] \[d = 2(R - r) = 2(8 - 3) = 10 \text{ cm}\]Outer diameter: 22 cm, hole diameter: 10 cm
2. Volume calculation
With R = 8 cm, r = 3 cm:
\[V = 2π^2 \cdot R \cdot r^2\] \[V = 2π^2 \cdot 8 \cdot 9\] \[V = 144π^2 ≈ 1421.3 \text{ cm}^3\]The volume is approximately 1421.3 cm³
3. Surface area calculation
With R = 8 cm, r = 3 cm:
\[S = 4π^2 \cdot R \cdot r\] \[S = 4π^2 \cdot 8 \cdot 3\] \[S = 96π^2 ≈ 947.5 \text{ cm}^2\]The surface area is approximately 947.5 cm²
4. Summary radii
The classic torus with radius input
Example 2: Input with diameters
5. Radius calculation
For D = 20 cm, d = 8 cm:
\[r = \frac{D - d}{4} = \frac{20 - 8}{4} = 3 \text{ cm}\] \[R = \frac{D}{2} - r = 10 - 3 = 7 \text{ cm}\]Major radius: 7 cm, minor radius: 3 cm
6. Volume from diameters
With R = 7 cm, r = 3 cm:
\[V = 2π^2 \cdot 7 \cdot 9\] \[V = 126π^2 ≈ 1243.6 \text{ cm}^3\]The volume is approximately 1243.6 cm³
7. Comparison of examples
R=8, r=3
V≈1421.3 cm³
R=7, r=3
V≈1243.6 cm³
ΔR=1 cm
ΔV≈177.7 cm³
With same tube radius r, a larger main radius R leads to significantly more volume
8. Practical application: O-ring
D = 22 mm
d = 10 mm
2r = 6 mm
≈ 1.42 cm³
A typical O-ring for industrial applications with calculated material consumption
9. Mathematical properties
π² ≈ 9.87
Torus characteristic
V/S = r/2
Elegant relationship
V ∝ R·r²
S ∝ R·r
The torus shows elegant mathematical relationships with the characteristic π² factor
The Torus: Classic perfection of geometry
The torus is one of the most elegant and practically significant forms of three-dimensional geometry. As a solid of revolution, created by rotating a circle around an axis outside the circle, it embodies mathematical purity and practical versatility in perfect harmony. Its characteristic donut shape with the central through hole makes it not only an aesthetically appealing object, but also a fundamental structure in engineering and science. From simple O-rings to architectural masterpieces to high-tech fusion reactors, the torus shows its universal applicability and timeless geometric beauty.
The geometry of rotation
The torus shows the elegance of perfect rotational geometry:
- Rotational origin: Rotation of a circle around an external axis
- Characteristic hole: Natural through hole by rotational geometry
- Double curvature: Both in meridional and equatorial direction
- π² elegance: Characteristic π² factor in volume and surface formulas
- Parametric clarity: Simple relationships between all dimensions
- Scaling properties: V ∝ R·r², S ∝ R·r with clear dependencies
- Topological significance: Genus-1 surface in algebraic topology
Versatile applications
Technical applications
O-rings, tires and tubes use the closed ring geometry for sealing and transport functions with optimal material distribution.
Scientific significance
In plasma physics, toroidal magnetic fields enable the confinement of fusion plasmas in tokamak reactors.
Architectural aesthetics
Modern architecture uses torus forms for spectacular buildings that combine functionality with visual impact.
Mathematical beauty
As a standard example in differential geometry and topology, the torus demonstrates fundamental mathematical concepts.
Summary
The torus embodies the perfect synthesis between mathematical elegance and practical functionality. Its creation by simple rotation of a circle leads to a form of remarkable versatility and beauty. The characteristic π² factors in its formulas underscore the deep mathematical structure of this geometry. From everyday O-rings to architectural masterpieces to high-tech fusion reactors, the torus shows its universal applicability. Its topological properties as a genus-1 surface make it a fundamental object of modern mathematics. The torus connects the purity of geometric forms with the power of practical applications and remains a timeless symbol for the elegance and universality of mathematical structures in our physical world.
|
|
|
|