Oloid Rechner
Rechner und Formeln zur Berechnung eines Oloids
Oloid Rechner
Das Oloid
Das Oloid ist die konvexe Hülle zweier senkrecht verbundener Kreise.
Oloid Eigenschaften
Das Oloid: Mathematisches Kunstwerk mit einzigartiger Geometrie
Oloid Visualisierung
Einzigartige Geometrie mit erstaunlichen Eigenschaften.
Rollkörper mit konstanter Breite.
|
|
Was ist ein Oloid?
Das Oloid ist ein außergewöhnlicher geometrischer Körper:
- Definition: Konvexe Hülle zweier verbundener kongruenter Kreise in senkrechten Ebenen
- Konstruktion: Mittelpunkt jedes Kreises liegt auf dem Rand des anderen
- Abstand: Kreismittelpunkte sind um einen Radius voneinander entfernt
- Besonderheit: Ein Drittel jedes Kreisumfangs liegt in der konvexen Hülle
- Eigenschaften: Rollkörper mit konstanter Breite und einzigartiger Form
- Anwendung: Kunst, Design, mechanische Anwendungen
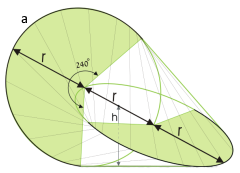
Geometrische Eigenschaften des Oloids
Das Oloid zeigt faszinierende geometrische Eigenschaften:
Grundparameter
- Radius r: Radius der beiden kongruenten Kreise
- Kantenlänge a: 4π/3 × r - Umfang der Kreisbögen
- Länge l: 3r - Maximale Ausdehnung
- Höhe h: 2r - Vertikale Ausdehnung
Besondere Eigenschaften
- Konvexe Hülle: Kleinste konvexe Form um beide Kreise
- Rollkörper: Rollt gleichmäßig auf ebenen Flächen
- Konstante Breite: Gleiche Ausdehnung in alle Richtungen
- Einzigartige Form: Mathematisch definierte Kunstform
Mathematische Beziehungen des Oloids
Das Oloid folgt exakten mathematischen Gesetzen:
Volumen-Formel
Das Volumen wird durch eine irrationale Konstante bestimmt. Näherungswert für praktische Berechnungen.
Oberflächen-Formel
Die Oberfläche entspricht der einer Kugel mit gleichem Radius - bemerkenswerte Eigenschaft!
Anwendungen des Oloids
Oloide finden Anwendung in verschiedenen Bereichen:
Kunst & Design
- Skulpturale Objekte
- Moderne Kunst
- Designelemente
- Architektonische Details
Mechanik & Technik
- Rollkörper-Anwendungen
- Mischanlagen
- Transportmechanismen
- Präzisionsmechanik
Bildung & Forschung
- Geometrie-Unterricht
- Mathematische Studien
- Forschungsobjekte
- Demonstrationen
Spielzeug & Spiele
- Lernspielzeug
- Puzzle-Elemente
- Physikalische Spiele
- Sammlerobjekte
Formeln zur Berechnung eines Oloids
Kantenlänge (a)
Umfang der Kreisbögen (4π/3 des Kreisumfangs)
Länge (l)
Maximale Ausdehnung des Oloids
Höhe (h)
Vertikale Ausdehnung des Oloids
Oberfläche (S)
Entspricht der Oberfläche einer Kugel mit Radius r
Volumen (V)*
*Das Volumen wird durch die irrationale Konstante 3.0524184684... als Näherung berechnet. Diese Konstante ist mathematisch exakt definiert, aber nicht durch einfache Brüche oder bekannte Konstanten darstellbar.
Besondere mathematische Eigenschaft
Bemerkenswert ist, dass die Oberfläche des Oloids (S = 4πr²) exakt der Oberfläche einer Kugel mit gleichem Radius entspricht, obwohl die Formen völlig unterschiedlich sind. Dies zeigt die elegante mathematische Struktur dieser außergewöhnlichen Geometrie.
Berechnungsbeispiel für ein Oloid
Gegeben
Gesucht: Alle Parameter des Oloids
1. Kantenlängen-Berechnung
Für r = 5 cm:
\[a = \frac{4π}{3} \cdot r\] \[a = \frac{4π}{3} \cdot 5\] \[a = \frac{20π}{3} ≈ 20.94 \text{ cm}\]Die Kantenlänge beträgt etwa 20.94 cm
2. Längen-Berechnung
Mit r = 5 cm:
\[l = 3 \cdot r = 3 \cdot 5\] \[l = 15 \text{ cm}\]Die maximale Länge beträgt 15 cm
3. Höhen-Berechnung
Mit r = 5 cm:
\[h = 2 \cdot r = 2 \cdot 5\] \[h = 10 \text{ cm}\]Die Höhe beträgt 10 cm
4. Oberflächen-Berechnung
Mit r = 5 cm:
\[S = 4π \cdot r^2 = 4π \cdot 25\] \[S = 100π ≈ 314.16 \text{ cm}^2\]Die Oberfläche beträgt etwa 314.16 cm²
5. Volumen-Berechnung
Mit r = 5 cm:
\[V = 3.0524184684 \cdot r^3\] \[V = 3.0524184684 \cdot 125\] \[V ≈ 381.55 \text{ cm}^3\]Das Volumen beträgt etwa 381.55 cm³
6. Zusammenfassung
Das Oloid mit Radius 5 cm
7. Vergleich mit Kugel
V = 381.55 cm³
S = 314.16 cm²
V = 523.60 cm³
S = 314.16 cm²
V: ≈ 72.9%
S: identisch!
Bemerkenswert: Gleiche Oberfläche wie Kugel, aber 27% weniger Volumen
8. Geometrische Verhältnisse
l/r = 15/5 = 3
h/r = 10/5 = 2
a/r = 4π/3 ≈ 4.19
Längliche Ellipse
Das Oloid zeigt harmonische Proportionen mit einfachen ganzzahligen Verhältnissen
Das Oloid: Mathematisches Kunstwerk der Geometrie
Das Oloid ist eines der faszinierendsten und zugleich rätselhaftesten geometrischen Objekte der modernen Mathematik. Als konvexe Hülle zweier senkrecht verbundener Kreise vereint es elegante Konstruktionslogik mit überraschenden mathematischen Eigenschaften. Seine bemerkenswerteste Eigenschaft - die identische Oberfläche mit einer Kugel gleichen Radius' trotz völlig unterschiedlicher Form - macht es zu einem wahren Wunder der Geometrie. Das Oloid demonstriert eindrucksvoll, wie aus einfachen Grundelementen komplexe und ästhetisch ansprechende Formen entstehen können, die sowohl mathematische Eleganz als auch praktische Anwendbarkeit besitzen.
Die Geometrie der Konvexität
Das Oloid zeigt die Schönheit konvexer Hüllen-Geometrie:
- Konvexe Hülle: Kleinste konvexe Form, die beide Kreise umschließt
- Senkrechte Kreise: Zwei kongruente Kreise in rechtwinkligen Ebenen
- Symmetrische Konstruktion: Mittelpunkt jedes Kreises auf dem Rand des anderen
- Rollkörper-Eigenschaften: Gleichmäßiges Rollen auf ebenen Flächen
- Konstante Breite: Gleiche Ausdehnung in verschiedene Richtungen
- Elegante Proportionen: Einfache ganzzahlige Verhältnisse (l=3r, h=2r)
- Einzigartige Ästhetik: Harmonische und organische Formgebung
Mathematische Besonderheiten
Oberflächen-Paradox
Die Oberfläche S = 4πr² ist identisch mit einer Kugel - eine der verblüffendsten Eigenschaften der Geometrie.
Irrationale Konstante
Das Volumen wird durch die irrationale Konstante ≈3.0524 bestimmt, die nicht durch einfache Formeln ausdrückbar ist.
Rollkörper-Mechanik
Als Rollkörper zeigt das Oloid einzigartige mechanische Eigenschaften für Transport- und Mischanwendungen.
Konstruktion-Eleganz
Die Konstruktion aus nur zwei Kreisen führt zu einer Form von außergewöhnlicher mathematischer und ästhetischer Komplexität.
Zusammenfassung
Das Oloid verkörpert die Verbindung zwischen mathematischer Präzision und künstlerischer Schönheit wie kaum ein anderer geometrischer Körper. Als konvexe Hülle zweier senkrecht verbundener Kreise zeigt es, wie aus einfachsten Grundelementen Formen von erstaunlicher Komplexität und Eleganz entstehen können. Seine paradoxe Eigenschaft - die identische Oberfläche mit einer Kugel trotz völlig unterschiedlicher Gestalt - macht es zu einem der faszinierendsten Objekte der modernen Geometrie. Von künstlerischen Skulpturen über mechanische Anwendungen bis hin zu mathematischen Forschungsobjekten zeigt das Oloid seine vielseitige Bedeutung. Es verbindet die Reinheit geometrischer Konstruktion mit der Rätselhaftigkeit mathematischer Konstanten und bleibt ein zeitloses Symbol für die Schönheit und das Geheimnis der dreidimensionalen Geometrie.
|
|
|
|