Paraboloid Rechner
Rechner und Formeln zur Berechnung eines Paraboloid
Paraboloid Rechner
Das Paraboloid
Das Paraboloid ist eine Fläche zweiter Ordnung, bekannt von Satellitenschüsseln und Reflektoren.
Paraboloid Eigenschaften
Das Paraboloid: Perfekte Fokussierung durch parabolische Krümmung
Paraboloid Visualisierung
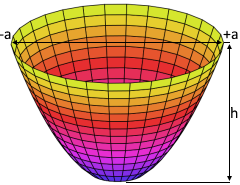
Das Paraboloid
Rotationsparaboloid mit perfekter Fokussierung
Perfekte Fokussierung paralleler Strahlen.
Grundlage moderner Reflektortechnik.
|
|
Was ist ein Paraboloid?
Das Paraboloid ist eine fundamentale geometrische Form:
- Definition: Fläche zweiter Ordnung durch Rotation einer Parabel
- Eigenschaften: Fokussiert parallele Strahlen in einem Brennpunkt
- Form: Schüssel- oder tellerförmige Oberfläche
- Anwendungen: Satellitenschüsseln, Reflektoren, Antennen
- Besonderheit: Perfekte optische und akustische Eigenschaften
- Technik: Grundlage moderner Kommunikationstechnik
Geometrische Eigenschaften des Paraboloids
Das Paraboloid zeigt einzigartige geometrische Eigenschaften:
Grundparameter
- Formparameter s: Bestimmt die Krümmung der Parabel
- Radius a: Radius der kreisförmigen Grundfläche
- Höhe h: h = s × a² - Abhängig von Form und Radius
- Rotationssymmetrie: Um die zentrale Achse
Besondere Eigenschaften
- Fokussierung: Parallele Strahlen treffen sich im Brennpunkt
- Reflexionseigenschaft: Perfekte Strahlenbündelung
- Skalierbarkeit: Von flachen bis zu tiefen Schüsseln
- Mathematische Eleganz: Definiert durch einfache quadratische Funktion
Mathematische Beziehungen des Paraboloids
Das Paraboloid folgt präzisen mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist die Hälfte eines Zylinders mit gleicher Grundfläche und Höhe.
Oberflächen-Formel
Die Oberfläche setzt sich aus Mantelfläche und kreisförmiger Grundfläche zusammen.
Anwendungen des Paraboloids
Paraboloide finden Anwendung in verschiedenen Bereichen:
Kommunikationstechnik
- Satellitenschüsseln
- Radar-Antennen
- Radioteleskope
- Richtfunk-Antennen
Optik & Beleuchtung
- Autoscheinwerfer
- Suchscheinwerfer
- Teleskop-Spiegel
- Solarkonzentratoren
Energietechnik
- Solarparabolspiegel
- Sonnenkollektoren
- Wärmekraftwerke
- Fokussier-Systeme
Architektur & Design
- Dachkonstruktionen
- Akustische Räume
- Skulpturale Elemente
- Moderne Architektur
Formeln zum Paraboloid
Höhe (h)
Höhe bestimmt durch Formparameter und Radius
Volumen (V)
Halbes Zylindervolumen
Mantelfläche (L)
Komplexe Formel für gekrümmte Oberfläche
Oberfläche (S)
Mantelfläche plus Grundkreis
Parabolische Gleichung
Die Grundgleichung des Rotationsparaboloids mit Formparameter s bestimmt die Krümmung der parabolischen Oberfläche. Für s > 0 öffnet sich die Parabel nach oben (konkave Form).
Berechnungsbeispiel für ein Paraboloid
Gegeben
Gesucht: Alle Parameter des Paraboloids
1. Höhen-Berechnung
Für s = 0.5, a = 4 cm:
\[h = s \cdot a^2\] \[h = 0.5 \cdot 16\] \[h = 8 \text{ cm}\]Die Höhe beträgt 8 cm
2. Volumen-Berechnung
Mit a = 4 cm, h = 8 cm:
\[V = \frac{1}{2} \cdot π \cdot a^2 \cdot h\] \[V = \frac{1}{2} \cdot π \cdot 16 \cdot 8\] \[V = 64π ≈ 201.06 \text{ cm}^3\]Das Volumen beträgt etwa 201.06 cm³
3. Mantelflächen-Berechnung
Mit a = 4 cm, h = 8 cm:
\[a^2 + 4h^2 = 16 + 256 = 272\] \[\sqrt{272} ≈ 16.49\] \[L = \frac{π \cdot 4}{6 \cdot 64} \cdot (272^{3/2} - 64)\] \[L ≈ 84.85 \text{ cm}^2\]Die Mantelfläche beträgt etwa 84.85 cm²
4. Gesamtoberflächen-Berechnung
Grundfläche + Mantelfläche:
\[A_{grund} = π \cdot a^2 = π \cdot 16 ≈ 50.27 \text{ cm}^2\] \[S = L + A_{grund}\] \[S = 84.85 + 50.27 ≈ 135.12 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 135.12 cm²
5. Zusammenfassung
Das Paraboloid mit Formparameter 0.5
6. Vergleich mit Zylinder
V = 201.06 cm³
V = 402.12 cm³
Das Paraboloid hat exakt die Hälfte des Zylindervolumens
7. Praktische Anwendung: Satellitenantenne
2a = 8 cm
h = 8 cm
Tiefe Schüssel
Sehr gut
Mit s = 0.5 entsteht eine relativ tiefe Parabolschüssel mit guter Fokussierung
8. Formparameter-Analyse
Mittlere Krümmung
h/(2a) = 1.0
Universell einsetzbar
Der Formparameter s = 0.5 erzeugt eine ausgewogene Parabolform
Das Paraboloid: Perfektion der Fokussierung
Das Paraboloid ist eine der wichtigsten und praktisch bedeutsamsten Flächen der analytischen Geometrie. Als Rotationsfläche einer Parabel vereint es mathematische Eleganz mit außergewöhnlichen physikalischen Eigenschaften. Seine bemerkenswerteste Eigenschaft - die perfekte Fokussierung paralleler Strahlen in einem einzigen Brennpunkt - macht es zur Grundlage unzähliger technischer Anwendungen. Von Satellitenschüsseln über Autoscheinwerfer bis hin zu Radioteleskopen nutzt moderne Technik die geometrische Perfektion des Paraboloids. Es demonstriert eindrucksvoll, wie mathematische Theorie zu praktischen Lösungen führt, die unseren Alltag prägen.
Die Geometrie der Fokussierung
Das Paraboloid zeigt die Perfektion fokussierender Geometrie:
- Fläche zweiter Ordnung: Durch quadratische Gleichung z = s(x²+y²) definiert
- Rotationssymmetrie: Entstehung durch Rotation einer Parabel um ihre Achse
- Fokussiereigenschaft: Alle parallelen Strahlen treffen sich im Brennpunkt
- Formparameter s: Bestimmt die Krümmung und damit die Fokussierstärke
- Skalierbarkeit: Von flachen Tellern bis zu tiefen Schüsseln
- Mathematische Eleganz: Einfache Gleichung mit komplexen Eigenschaften
- Universelle Anwendung: Optik, Akustik, Elektromagnetismus
Technische Bedeutung
Kommunikationstechnik
Satellitenschüsseln und Radar-Antennen nutzen die Fokussiereigenschaft für maximale Signalstärke und Richtwirkung.
Energietechnik
Solarkonzentratoren und Parabolspiegel bündeln Sonnenlicht für effiziente Energiegewinnung.
Optische Systeme
Teleskope und Scheinwerfer verwenden parabolische Spiegel für perfekte Strahlformung und Lichtsammlung.
Akustische Anwendungen
Parabolische Reflektoren in Mikrofonen und Lautsprechern nutzen die Fokussierung für optimale Schallübertragung.
Zusammenfassung
Das Paraboloid verkörpert die perfekte Vereinigung von mathematischer Theorie und technischer Praxis. Als Fläche zweiter Ordnung zeigt es, wie einfache quadratische Beziehungen zu außergewöhnlichen physikalischen Eigenschaften führen können. Seine Fokussiereigenschaft - die perfekte Bündelung paralleler Strahlen in einem Brennpunkt - macht es zu einem fundamentalen Baustein moderner Technik. Von der Satellitenantenne auf dem Dach über den Scheinwerfer im Auto bis zum Radioteleskop in der Forschung nutzen unzählige Anwendungen die geometrische Perfektion des Paraboloids. Es verbindet die Eleganz mathematischer Formen mit der Kraft physikalischer Gesetze und bleibt ein zeitloses Beispiel dafür, wie Geometrie unsere technologische Welt formt und ermöglicht.
|
|
|
|