Spindeltorus Rechner
Rechner und Formeln zur Berechnung eines Spindeltorus
Spindeltorus Rechner
Der Spindeltorus
Der Spindeltorus ist ein Torus-Typ mit Einbuchtung statt Loch.
Spindeltorus Eigenschaften
Der Spindeltorus: Torus ohne Durchgangsloch
Spindeltorus Visualisierung
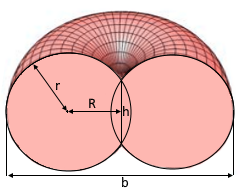
Spindeltorus Querschnitt
Zeigt die charakteristische Einbuchtung
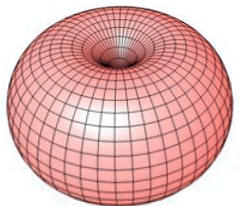
Spindeltorus 3D-Ansicht
Vollständige dreidimensionale Form
Torus ohne Durchgangsloch.
Charakteristische spindelförmige Gestalt.
|
|
Was ist ein Spindeltorus?
Der Spindeltorus ist eine besondere Art des Torus:
- Definition: Torus bei dem der Abstand R kleiner ist als der Röhrenradius r
- Charakteristikum: Kein Durchgangsloch, nur eine Einbuchtung in der Mitte
- Form: Spindelähnliche, birnenförmige Gestalt
- Bedingung: R < r (Abstand kleiner als Röhrenradius)
- Entstehung: Rotation eines Kreises um eine Achse bei geringem Abstand
- Anwendung: Design, Architektur, Maschinenbau
Geometrische Eigenschaften des Spindeltorus
Der Spindeltorus zeigt spezielle geometrische Eigenschaften:
Grundparameter
- Abstand R: Distanz vom Röhrenmittelpunkt zum Torus-Zentrum
- Röhrenradius r: Radius des rotierenden Kreises
- Bedingung: R < r für Spindeltorus-Formation
- Innenhöhe h: h = 2√(r²-R²) - Höhe der Einbuchtung
Besondere Eigenschaften
- Kein Loch: Im Gegensatz zum normalen Torus geschlossen
- Einbuchtung: Charakteristische Vertiefung in der Mitte
- Spindelform: Birnen- oder spindelähnliche Gesamtgestalt
- Rotationssymmetrie: Symmetrisch um die zentrale Achse
Mathematische Beziehungen des Spindeltorus
Der Spindeltorus folgt komplexen mathematischen Gesetzen:
Innenhöhe-Formel
Die Innenhöhe hängt vom Verhältnis zwischen Röhrenradius und Abstand ab.
Volumen-Formel
Das Volumen erfordert Integration über elliptische Funktionen.
Anwendungen des Spindeltorus
Spindeltori finden Anwendung in verschiedenen Bereichen:
Design & Kunst
- Skulpturale Formen
- Moderne Architektur
- Produktdesign
- Keramik und Töpferei
Technik & Industrie
- Druckbehälter
- Maschinenbauteile
- Strömungstechnik
- Verfahrenstechnik
Architektur & Bau
- Kuppelkonstruktionen
- Brückenbau
- Tunnelbau
- Sonderbauformen
Wissenschaft & Forschung
- Topologie-Studien
- Materialwissenschaft
- Biomechanik
- Geometrische Analysis
Formeln zum Spindeltorus
Breite (b)
Maximale Breite des Spindeltorus
Innenhöhe (h)
Höhe der mittleren Einbuchtung
Volumen (V)
Komplexe Volumenformel mit elliptischen Integralen
Spindeltorus Bedingung
Für die Existenz eines Spindeltorus muss gelten: R < r
Wenn R ≥ r, entsteht ein normaler Torus mit Loch oder ein Ring-Torus.
Bei R = 0 ergibt sich eine Kugel mit Radius r.
Berechnungsbeispiel für einen Spindeltorus
Gegeben
Gesucht: Alle Parameter des Spindeltorus
1. Bedingung prüfen
Für Spindeltorus: R < r
R = 3 cm, r = 5 cm
3 < 5 ✓ Bedingung erfüllt!
Es entsteht ein Spindeltorus ohne Loch
2. Breiten-Berechnung
Mit R = 3 cm, r = 5 cm:
\[b = 2 \cdot (R + r)\] \[b = 2 \cdot (3 + 5)\] \[b = 2 \cdot 8 = 16 \text{ cm}\]Die maximale Breite beträgt 16 cm
3. Innenhöhen-Berechnung
Mit r = 5 cm, R = 3 cm:
\[h = 2 \cdot \sqrt{r^2 - R^2}\] \[h = 2 \cdot \sqrt{25 - 9}\] \[h = 2 \cdot \sqrt{16} = 2 \cdot 4 = 8 \text{ cm}\]Die Innenhöhe der Einbuchtung beträgt 8 cm
4. Volumen-Berechnung (Teil 1)
Erster Term:
\[V_1 = \frac{2π}{3} \cdot (2r^2 + R^2) \cdot \sqrt{r^2 - R^2}\] \[V_1 = \frac{2π}{3} \cdot (50 + 9) \cdot 4\] \[V_1 = \frac{2π \cdot 59 \cdot 4}{3} ≈ 494.8 \text{ cm}^3\]Erster Volumen-Teil berechnet
5. Volumen-Berechnung (Teil 2)
Zweiter Term mit arctan:
\[\arctan\left(\frac{3}{4}\right) ≈ 0.6435 \text{ rad}\] \[V_2 = π \cdot 25 \cdot 3 \cdot (π + 2 \cdot 0.6435)\] \[V_2 ≈ 75π \cdot 4.4305 ≈ 1043.9 \text{ cm}^3\]Zweiter Volumen-Teil mit elliptischem Integral
6. Gesamtvolumen
Summe beider Terme:
\[V = V_1 + V_2\] \[V ≈ 494.8 + 1043.9\] \[V ≈ 1538.7 \text{ cm}^3\]Das Gesamtvolumen beträgt etwa 1538.7 cm³
7. Zusammenfassung
Der Spindeltorus mit charakteristischer Einbuchtung
8. Vergleich mit anderen Formen
V = 1538.7 cm³
Kein Loch
V = 523.6 cm³
Kompakt
≈ 2.94× größer
Spindelform
Der Spindeltorus hat fast dreimal das Volumen einer Kugel mit gleichem Röhrenradius
9. Geometrische Analyse
3/5 = 0.6
h/b = 8/16 = 0.5
Mittlere Einbuchtung
Ausgeprägte Spindel
Bei R/r = 0.6 entsteht eine deutlich ausgeprägte Spindelform ohne Durchgangsloch
Der Spindeltorus: Geometrie ohne Loch
Der Spindeltorus ist eine faszinierende geometrische Form, die eine besondere Stellung in der Familie der Torus-Körper einnimmt. Als einziger Torus-Typ ohne Durchgangsloch demonstriert er, wie kleine Parameteränderungen zu völlig unterschiedlichen geometrischen Eigenschaften führen können. Die entscheidende Bedingung R < r führt dazu, dass sich die rotierende Röhre selbst überlappt und eine charakteristische Einbuchtung statt eines Lochs bildet. Diese elegante Form findet nicht nur in der reinen Mathematik Beachtung, sondern auch in praktischen Anwendungen von der Architektur bis zum Maschinenbau, wo die Kombination aus struktureller Integrität und ästhetischer Anziehungskraft geschätzt wird.
Die Geometrie der Einbuchtung
Der Spindeltorus zeigt die Eleganz geschlossener Torus-Geometrie:
- Charakteristische Bedingung: R < r führt zu Selbstüberlappung der Röhre
- Kein Durchgangsloch: Im Gegensatz zum klassischen Torus geschlossen
- Zentrale Einbuchtung: Charakteristische Vertiefung mit Höhe h = 2√(r²-R²)
- Spindelform: Birnen- oder spindelähnliche Gesamtgestalt
- Maximale Breite: b = 2(R+r) - einfache lineare Beziehung
- Rotationssymmetrie: Perfekte Symmetrie um die zentrale Achse
- Parameterkontinuität: Glatter Übergang zu anderen Torus-Formen
Mathematische Komplexität
Volumen-Integration
Die Volumenformel erfordert elliptische Integrale und Arkustangens-Funktionen, was die mathematische Eleganz dieser Form unterstreicht.
Geometrische Übergänge
Bei R → 0 wird der Spindeltorus zur Kugel, bei R → r entsteht der Übergang zum klassischen Torus - kontinuierliche Transformation.
Strukturelle Eigenschaften
Die geschlossene Form ohne Loch bietet hervorragende strukturelle Integrität für technische Anwendungen.
Ästhetische Wirkung
Die organische, spindelförmige Gestalt macht den Spindeltorus zu einer bevorzugten Form in Design und Architektur.
Zusammenfassung
Der Spindeltorus verkörpert die faszinierende Vielfalt geometrischer Formen, die aus einfachen Rotationsprinzipien entstehen können. Als einziger Torus ohne Durchgangsloch zeigt er, wie die Variation eines Parameters - des Verhältnisses R/r - zu völlig neuen geometrischen Eigenschaften führt. Seine charakteristische Einbuchtung statt eines Lochs macht ihn nicht nur mathematisch interessant, sondern auch praktisch wertvoll für Anwendungen, die strukturelle Geschlossenheit erfordern. Von skulpturalen Kunstwerken über architektonische Elemente bis hin zu technischen Komponenten zeigt der Spindeltorus seine Vielseitigkeit. Er verbindet die Reinheit mathematischer Definitionen mit der Schönheit organischer Formen und bleibt ein eindrucksvolles Beispiel dafür, wie Geometrie sowohl intellektuell faszinierend als auch ästhetisch ansprechend sein kann.
|
|
|
|