Triaxiales Ellipsoid Rechner
Rechner und Formeln zur Berechnung von Volumen und Oberfläche eines triaxialen Ellipsoids
Triaxiales Ellipsoid Rechner
Das Triaxiale Ellipsoid
Das triaxiale Ellipsoid ist ein dreiachsiger Körper mit drei unterschiedlichen Halbachsen a, b und c.
Triaxiales Ellipsoid Eigenschaften
Der dreiachsige Körper: Drei unterschiedliche Halbachsen
Triaxiales Ellipsoid
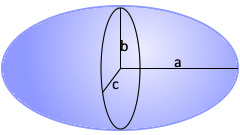
Das allgemeinste Ellipsoid mit drei Achsen.
Maximale geometrische Flexibilität.
|
|
Was ist ein triaxiales Ellipsoid?
Das triaxiale Ellipsoid ist die allgemeinste Form eines Ellipsoids:
- Definition: Ellipsoid mit drei unterschiedlichen Halbachsen
- Achsen: a, b und c sind alle verschieden
- Symmetrie: Keine Rotationssymmetrie
- Flexibilität: Maximale geometrische Anpassungsfähigkeit
- Komplexität: Oberfläche nur näherungsweise berechenbar
- Anwendung: Kristalle, Moleküle, astronomische Objekte
Geometrische Eigenschaften des triaxialen Ellipsoids
Das triaxiale Ellipsoid zeigt einzigartige geometrische Eigenschaften:
Grundparameter
- Halbachsen: a, b, c (alle verschieden)
- Hauptschnitte: Drei verschiedene Ellipsen
- Symmetrieebenen: Drei orthogonale Ebenen
- Mittelpunktsymmetrie: Punktsymmetrisch zum Zentrum
Besondere Eigenschaften
- Komplexe Krümmung: Variiert in alle Richtungen
- Elliptische Querschnitte: Alle Schnitte sind Ellipsen
- Maximale Flexibilität: Anpassung an beliebige Formen
- Keine Rotationssymmetrie: Allgemeinster Ellipsoid-Typ
Mathematische Beziehungen
Das triaxiale Ellipsoid folgt komplexen mathematischen Gesetzen:
Volumen-Formel
Einfache Formel mit drei Halbachsen. Elegant und präzise.
Oberflächen-Formel
Knud Thomsen Approximation. Maximaler Fehler: 1.061%.
Anwendungen des triaxialen Ellipsoids
Triaxiale Ellipsoide finden Anwendung in verschiedenen Bereichen:
Kristallographie
- Kristallstrukturen
- Mineralogische Formen
- Gitterparameter
- Anisotrope Eigenschaften
Astronomie
- Asteroidenformen
- Irreguläre Himmelskörper
- Galaxienmodellierung
- Gravitationsfelder
Molekularphysik
- Molekülgeometrie
- Elektronendichteverteilung
- Schwingungsellipsoide
- Anisotrope Tensor
Technik & Design
- CAD-Modellierung
- 3D-Objekte
- Formoptimierung
- Materialwissenschaft
Formeln zum triaxialen Ellipsoid
Volumen (V)
Exakte Formel für das Volumen
Oberfläche (S) - Näherung
Knud Thomsen Näherungsformel
Parameter p
Optimaler Exponent für minimalen Fehler
Genauigkeit
Sehr hohe Genauigkeit für praktische Anwendungen
Ellipsoid Gleichung
Standardform der triaxialen Ellipsoid-Gleichung im Koordinatensystem
Berechnungsbeispiel für ein triaxiales Ellipsoid
Gegeben
Gesucht: Volumen und Oberfläche des triaxialen Ellipsoids
2. Oberflächen-Berechnung (Näherung)
Mit p = 1.6075:
\[a^p = 6^{1.6075} ≈ 13.86\] \[b^p = 4^{1.6075} ≈ 7.73\] \[c^p = 3^{1.6075} ≈ 5.29\] \[S ≈ 4\pi \left( \frac{13.86 \cdot 7.73 + 13.86 \cdot 5.29 + 7.73 \cdot 5.29}{3} \right)^{1/1.6075}\] \[S ≈ 226.24 \text{ cm}^2\]Die Oberfläche beträgt etwa 226.24 cm²
1. Volumen-Berechnung
Für a = 6, b = 4, c = 3:
\[V = \frac{4}{3} \cdot \pi \cdot 6 \cdot 4 \cdot 3\] \[V = \frac{4}{3} \cdot \pi \cdot 72\] \[V = 96\pi\] \[V ≈ 301.59 \text{ cm}^3\]Das Volumen beträgt etwa 301.59 cm³
3. Ellipsoid-Analyse
Verhältnisse der Achsen:
\[\frac{a}{b} = \frac{6}{4} = 1.5\] \[\frac{a}{c} = \frac{6}{3} = 2.0\] \[\frac{b}{c} = \frac{4}{3} ≈ 1.33\]Alle Achsen unterschiedlich → triaxial
Typisches triaxiales Ellipsoid mit drei verschiedenen Achsen
4. Das triaxiale Ellipsoid
Das allgemeinste Ellipsoid mit drei verschiedenen Achsen
Das triaxiale Ellipsoid: Höchste geometrische Flexibilität
Das triaxiale Ellipsoid ist die allgemeinste Form eines Ellipsoids und verkörpert maximale geometrische Flexibilität. Mit drei unterschiedlichen Halbachsen a, b und c kann es nahezu jede ellipsoidale Form annehmen und findet daher breite Anwendung in Wissenschaft und Technik. Während das Volumen exakt berechenbar ist, erfordert die Oberflächenberechnung raffinierte Näherungsverfahren wie die elegante Knud Thomsen Formel, die mit minimaler Abweichung praktisch exakte Ergebnisse liefert.
Die Geometrie der drei Achsen
Das triaxiale Ellipsoid zeigt die Komplexität und Schönheit der dreidimensionalen Geometrie:
- Drei Hauptachsen: a, b und c sind alle verschieden und orthogonal
- Keine Rotationssymmetrie: Kein Rotationsellipsoid möglich
- Drei Symmetrieebenen: Orthogonale Spiegelebenen durch das Zentrum
- Elliptische Querschnitte: Jeder Schnitt durch das Zentrum ist eine Ellipse
- Komplexe Krümmung: Krümmung variiert in alle Raumrichtungen
- Maximale Anpassung: Optimale Anpassung an beliebige Formen
- Universelle Anwendung: Von Molekülen bis zu Galaxien
Mathematische Komplexität und Eleganz
Volumen-Einfachheit
Trotz der geometrischen Komplexität ist die Volumenformel elegant einfach - das Produkt aller drei Halbachsen mit dem π-Faktor.
Oberflächen-Herausforderung
Die Oberflächenberechnung erfordert elliptische Integrale. Knud Thomsens Näherungsformel bietet eine brillante praktische Lösung.
Wissenschaftliche Präzision
Mit weniger als 1.1% Abweichung ermöglicht die Näherungsformel präzise Berechnungen für alle praktischen Anwendungen.
Universelle Bedeutung
Als allgemeinste Ellipsoid-Form ist das triaxiale Ellipsoid fundamental für die Beschreibung komplexer dreidimensionaler Objekte.
Zusammenfassung
Das triaxiale Ellipsoid repräsentiert die Vollendung der Ellipsoid-Geometrie durch seine drei unterschiedlichen Halbachsen und die daraus resultierende maximale Formflexibilität. Seine elegante Volumenformel kontrastiert mit der komplexen Oberflächenberechnung, die durch Knud Thomsens geniale Näherungsformel praktisch lösbar wird. Von der Kristallographie über die Astronomie bis zur Molekularphysik ermöglicht das triaxiale Ellipsoid die präzise Beschreibung komplexester dreidimensionaler Strukturen. Als universelles Werkzeug der geometrischen Modellierung verbindet es mathematische Eleganz mit praktischer Anwendbarkeit und zeigt, wie die Kombination von drei einfachen Parametern zu unendlicher geometrischer Vielfalt führen kann.
|
|
|
|