Raumwinkel Rechner
Rechner und Formel zur Berechnung von Raumwinkel in Steradiant
Raumwinkel Rechner
Der Raumwinkel
Der Raumwinkel ist das Verhältnis der ausgeschnittenen Fläche zum Quadrat des Radius.
Raumwinkel Eigenschaften
Der Raumwinkel: Dreidimensionale Erweiterung des ebenen Winkels
Raumwinkel Visualisierung
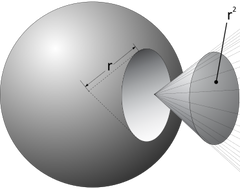
Der Raumwinkel
Dreidimensionale Winkelmessung in Steradiant
Maß für den Anteil einer Kugeloberfläche.
Einheit: Steradiant (sr) - dimensionslos.
|
|
Was ist ein Raumwinkel?
Der Raumwinkel ist ein fundamentales geometrisches Konzept:
- Definition: Verhältnis der ausgeschnittenen Kugelkalotte zum Quadrat des Radius
- Einheit: Steradiant (sr) - dimensionslose SI-Einheit
- Analogie: Dreidimensionale Erweiterung des ebenen Winkels
- Vollkugel: 4π Steradiant (≈ 12.57 sr)
- Halbkugel: 2π Steradiant (≈ 6.28 sr)
- Anwendung: Optik, Beleuchtung, Astronomie, Physik
Geometrische Eigenschaften des Raumwinkels
Der Raumwinkel zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Kalottenfläche A: Ausgeschnittene Fläche auf der Kugeloberfläche
- Kugelradius r: Radius der Bezugskugel
- Raumwinkel Ω: Ω = A / r² (in Steradiant)
- Dimensionslosigkeit: [sr] = [m²]/[m²] = dimensionslos
Besondere Eigenschaften
- Radiusunabhängig: Verhältnis bleibt bei Skalierung konstant
- Additivität: Raumwinkel können addiert werden
- Vollkugel-Referenz: 4π sr für die gesamte Kugeloberfläche
- Kegelförmige Projektion: Entspricht einem Kegel vom Zentrum
Mathematische Beziehungen des Raumwinkels
Der Raumwinkel folgt einfachen mathematischen Gesetzen:
Grundformel
Der Raumwinkel ist das Verhältnis der Kalottenfläche zum Quadrat des Radius.
Vollkugel-Referenz
Die gesamte Kugeloberfläche entspricht einem Raumwinkel von 4π Steradiant.
Anwendungen des Raumwinkels
Raumwinkel finden Anwendung in verschiedenen Bereichen:
Optik & Beleuchtung
- Lichtstärke-Berechnungen
- Beleuchtungstechnik
- Lichtverteilung
- Photometrie
Astronomie & Astrophysik
- Himmelskörper-Beobachtung
- Teleskop-Sichtfelder
- Strahlungsverteilung
- Satellitennavigation
Physik & Technik
- Strahlungsphysik
- Kernphysik
- Detektortechnik
- Antennentechnik
Bildgebung & Computer Vision
- Kamera-Sichtfelder
- 3D-Computer-Vision
- Bildverarbeitung
- Robotik
Formeln zum Raumwinkel
Raumwinkel (Ω)
Wobei A die Kalottenfläche und r der Kugelradius ist. Der Raumwinkel wird in Steradiant (sr) gemessen.
Kalottenfläche (A)
Fläche der Kugelkalotte aus Raumwinkel
Kugelradius (r)
Radius aus Fläche und Raumwinkel
Wichtige Raumwinkel-Werte
4π sr ≈ 12.57 sr
2π sr ≈ 6.28 sr
π sr ≈ 3.14 sr
≈ 7.96% der Vollkugel
Berechnungsbeispiele für Raumwinkel
Beispiel 1: Raumwinkel berechnen
1. Raumwinkel-Berechnung
Für A = 50 cm², r = 10 cm:
\[\Omega = \frac{A}{r^2} = \frac{50}{10^2}\] \[\Omega = \frac{50}{100} = 0.5 \text{ sr}\]Der Raumwinkel beträgt 0.5 Steradiant
2. Prozent der Vollkugel
Anteil an der Vollkugel:
\[\text{Anteil} = \frac{\Omega}{4\pi} \times 100\%\] \[\text{Anteil} = \frac{0.5}{4\pi} \times 100\%\] \[\text{Anteil} ≈ 3.98\%\]Die Kalotte umfasst etwa 3.98% der Kugeloberfläche
Beispiel 2: Kalottenfläche berechnen
3. Kalottenflächen-Berechnung
Für Ω = 1.0 sr, r = 8 cm:
\[A = \Omega \times r^2\] \[A = 1.0 \times 8^2\] \[A = 1.0 \times 64 = 64 \text{ cm}^2\]Die Kalottenfläche beträgt 64 cm²
4. Bedeutung von 1 Steradiant
1 sr entspricht:
\[\frac{1 \text{ sr}}{4\pi \text{ sr}} = \frac{1}{4\pi} ≈ 7.96\%\]der gesamten Kugeloberfläche
1 Steradiant ist etwa 1/12.57 der Vollkugel
Beispiel 3: Kugelradius berechnen
5. Radius-Berechnung
Für A = 100 cm², Ω = 0.8 sr:
\[r = \sqrt{\frac{A}{\Omega}} = \sqrt{\frac{100}{0.8}}\] \[r = \sqrt{125} ≈ 11.18 \text{ cm}\]Der Kugelradius beträgt etwa 11.18 cm
6. Verifikation
Kontrolle:
\[\Omega = \frac{A}{r^2} = \frac{100}{11.18^2}\] \[\Omega = \frac{100}{125} = 0.8 \text{ sr} ✓\]Die Berechnung ist korrekt
7. Praktische Anwendungen
Lichtkegel-Berechnungen
Teleskop-Sichtfelder
Linsen-Akzeptanzwinkel
Abstrahlcharakteristik
Raumwinkel sind in vielen technischen Bereichen fundamental
Der Raumwinkel: Dreidimensionale Winkelmessung
Der Raumwinkel ist eine der elegantesten und praktisch bedeutsamsten Erweiterungen des klassischen Winkelbegriffs in die dritte Dimension. Als Verhältnis einer Kugelkalottenfläche zum Quadrat des Kugelradius definiert, stellt er ein dimensionsloses Maß dar, das unabhängig von der Größe der Bezugskugel ist. Diese bemerkenswerte Eigenschaft macht ihn zu einem universellen Werkzeug in Physik, Technik und Astronomie. Von der Berechnung von Lichtstärken in der Beleuchtungstechnik über die Charakterisierung von Teleskop-Sichtfeldern bis hin zur Beschreibung von Strahlungsverteilungen zeigt der Raumwinkel seine fundamentale Bedeutung für unser Verständnis dreidimensionaler Geometrie und physikalischer Phänomene.
Die Geometrie der Dimensionslosigkeit
Der Raumwinkel zeigt die Eleganz dimensionsloser Geometrie:
- Dreidimensionale Erweiterung: Natürliche Verallgemeinerung des ebenen Winkels
- Dimensionslosigkeit: [A]/[r²] = [m²]/[m²] = dimensionslos
- Skalierungsinvarianz: Verhältnis bleibt bei beliebiger Größenänderung konstant
- SI-Einheit Steradiant: Offiziell anerkannte, aber abgeleitete Einheit
- Vollkugel-Normierung: 4π Steradiant für die gesamte Kugeloberfläche
- Geometrische Intuition: Kegelförmige Projektion vom Mittelpunkt
- Additivität: Raumwinkel benachbarter Bereiche addieren sich
Wissenschaftliche und technische Bedeutung
Optik und Beleuchtung
In der Photometrie beschreibt der Raumwinkel die Ausbreitung von Licht und ermöglicht präzise Berechnungen von Beleuchtungsstärken.
Astronomie und Astrophysik
Teleskop-Sichtfelder, Strahlungsverteilungen von Sternen und die Charakterisierung astronomischer Instrumente nutzen Raumwinkel-Konzepte.
Strahlungsphysik
Die Beschreibung von Teilchenstrahlung, Kernzerfällen und Detektorgeometrien basiert fundamental auf Raumwinkel-Berechnungen.
Moderne Technologien
Computer Vision, Robotik und Antennentechnik verwenden Raumwinkel für Sichtfeld-Analysen und Strahlungscharakteristiken.
Zusammenfassung
Der Raumwinkel verkörpert die perfekte Brücke zwischen geometrischer Abstraktion und praktischer Anwendung. Als dimensionslose Größe zeigt er, wie mathematische Konzepte universelle Gültigkeit erlangen können, unabhängig von Maßstäben oder spezifischen Einheiten. Seine einfache Definition Ω = A/r² verbirgt eine tiefe geometrische Wahrheit: Die Form eines Raumbereichs lässt sich durch das Verhältnis seiner Projektion charakterisieren. Von der Quantifizierung von Lichtstrahlen über die Beschreibung astronomischer Sichtfelder bis hin zur Charakterisierung moderner Sensorsysteme zeigt der Raumwinkel seine universelle Bedeutung. Er verbindet die Reinheit geometrischer Konzepte mit der Kraft physikalischer Anwendungen und bleibt ein fundamentales Werkzeug für das Verständnis unserer dreidimensionalen Welt und der in ihr wirkenden Phänomene.
|
|
|
|