Kugelschale Rechner
Rechner und Formeln zur Berechnung einer Kugelschale
Kugelschale Rechner
Die Kugelschale
Die Kugelschale (auch Hohlkugel genannt) entsteht durch einen kugelförmigen Hohlraum in einer größeren Kugel.
Kugelschale Eigenschaften
Die Kugelschale: Hohlraum mit konstanter Wandstärke
Kugelschale Visualisierung
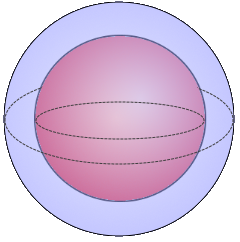
Die Kugelschale
Hohlkugel mit konstanter Wandstärke
Optimale Materialverteilung bei Hohlkugeln.
Leicht aber stabil.
|
|
Was ist eine Kugelschale?
Die Kugelschale ist ein spezieller geometrischer Körper:
- Definition: Hohlkugel mit kugelförmigem Hohlraum im Inneren
- Struktur: Große Kugel minus kleinere konzentrische Kugel
- Wandstärke: Konstante Dicke a = R - r
- Materialeffizienz: Maximale Stabilität bei minimalem Material
- Anwendung: Druckbehälter, Kugellager, Architektur
- Besonderheit: Doppelte Oberflächenberechnung (innen + außen)
Geometrische Eigenschaften der Kugelschale
Die Kugelschale zeigt einzigartige geometrische Eigenschaften:
Grundparameter
- Außenradius R: Radius der äußeren Kugeloberfläche
- Innenradius r: Radius des kugelförmigen Hohlraums
- Schalendicke a: Wandstärke a = R - r
- Konzentrizität: Beide Kugeln haben den gleichen Mittelpunkt
Besondere Eigenschaften
- Doppelte Oberfläche: Außen- plus Innenfläche
- Materialeffizienz: Optimales Verhältnis Stabilität/Gewicht
- Skalierbarkeit: Von dünner Schale bis dicker Wand
- Symmetrie: Vollständige sphärische Symmetrie
Mathematische Beziehungen der Kugelschale
Die Kugelschale folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Schalenvolumen als Differenz zweier Kugeln. Elegante Kubik-Differenz-Formel.
Oberflächen-Formel
Die Gesamtoberfläche als Summe beider Kugelflächen. Innen- plus Außenoberfläche.
Anwendungen der Kugelschale
Kugelschalen finden Anwendung in verschiedenen Bereichen:
Maschinenbau & Technik
- Druckbehälter und Tanks
- Kugellager (Hohlkugeln)
- Leichtbaukonstruktionen
- Präzisionsmechanik
Luft- & Raumfahrt
- Satellitentanks
- Druckkabinen
- Leichtbau-Strukturen
- Brennstofftanks
Architektur & Bau
- Kuppelkonstruktionen
- Moderne Architektur
- Skulpturale Elemente
- Leichtbau-Dächer
Wissenschaft & Forschung
- Hochdruck-Experimente
- Materialforschung
- Physikalische Modelle
- Biomechanik
Formeln zur Kugelschale
Schalendicke (a)
Differenz zwischen Außen- und Innenradius
Volumen der Schale (V)
Differenz der Kugelvolumina
Oberfläche (S)
Summe aus Außen- und Innenfläche
Einzeloberflächen
Außen- und Innenfläche einzeln
Geometrische Beziehungen
\(R > r > 0\)
\(a = R - r\)
Optimal bei dünnen Wänden
Der Außenradius muss größer als der Innenradius sein
Berechnungsbeispiel für eine Kugelschale
Gegeben
Gesucht: Alle Parameter der Kugelschale
1. Schalendicken-Berechnung
Für R = 10 cm, r = 7 cm:
\[a = R - r = 10 - 7\] \[a = 3 \text{ cm}\]Die Schalendicke beträgt 3 cm
2. Volumen-Berechnung
Mit R = 10 cm, r = 7 cm:
\[V = \frac{4π}{3} \cdot (R^3 - r^3)\] \[V = \frac{4π}{3} \cdot (1000 - 343)\] \[V = \frac{4π}{3} \cdot 657 ≈ 2753.8 \text{ cm}^3\]Das Schalenvolumen beträgt etwa 2753.8 cm³
3. Oberflächen-Berechnung
Mit R = 10 cm, r = 7 cm:
\[S = 4π \cdot (R^2 + r^2)\] \[S = 4π \cdot (100 + 49)\] \[S = 4π \cdot 149 ≈ 1870.8 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 1870.8 cm²
4. Einzeloberflächen
Aufgeteilt nach innen/außen:
\[S_{außen} = 4π \cdot 10^2 = 400π ≈ 1256.6 \text{ cm}^2\] \[S_{innen} = 4π \cdot 7^2 = 196π ≈ 615.8 \text{ cm}^2\]Außenfläche: 1256.6 cm², Innenfläche: 615.8 cm²
5. Zusammenfassung
Die Kugelschale mit 3 cm Wandstärke
6. Vergleich mit Vollkugel
V = 2753.8 cm³
V = 4188.8 cm³
Die Hohlkugel spart etwa 1/3 Material
7. Materialeffizienz-Analyse
a/R = 3/10 = 0.3
r³/R³ = 34.3%
Mittlere Wandstärke
Sehr gute Balance
Optimale Balance zwischen Stabilität und Materialersparnis
Die Kugelschale: Materialeffizienz durch Geometrie
Die Kugelschale ist ein faszinierender geometrischer Körper, der die Eleganz der Kugelgeometrie mit den Prinzipien der Materialeffizienz verbindet. Als Hohlkugel mit konstanter Wandstärke zeigt sie, wie durch geschickte geometrische Gestaltung maximale Stabilität bei minimalem Materialeinsatz erreicht werden kann. Die mathematische Schönheit liegt in den eleganten Differenz-Formeln für Volumen (R³-r³) und Summen-Formeln für Oberflächen (R²+r²), die das Wesen der Hohlkugel perfekt beschreiben.
Die Geometrie der Effizienz
Die Kugelschale zeigt die Perfektion materialsparender Geometrie:
- Doppelte Oberfläche: Innen- und Außenfläche für maximale Funktionalität
- Konstante Wandstärke: Gleichmäßige Materialverteilung und Stabilität
- Sphärische Symmetrie: Optimale Druckverteilung in alle Richtungen
- Materialeffizienz: Maximale Stabilität bei minimalem Gewicht
- Skalierbarkeit: Von dünnen Schalen bis dicken Wänden
- Elegante Mathematik: Einfache Differenz- und Summenformeln
- Universelle Anwendung: Von Mikrotechnik bis Großbehältern
Mathematische Eleganz
Differenz-Formeln
Die Volumenformel V = 4π/3 × (R³-r³) zeigt die elegante Kubik-Differenz, die das Wesen der Hohlkugel mathematisch erfasst.
Summen-Formeln
Die Oberflächenformel S = 4π × (R²+r²) addiert elegant Innen- und Außenfläche zu einer Gesamtoberfläche.
Materialoptimierung
Die Kugelschale ermöglicht Materialersparnisse von 20-80% gegenüber Vollkugeln bei erhaltener struktureller Integrität.
Technische Perfektion
In Druckbehältern, Kugeltanks und Leichtbau zeigt die Kugelschale ihre technische Überlegenheit durch optimale Spannungsverteilung.
Zusammenfassung
Die Kugelschale verkörpert die perfekte Harmonie zwischen geometrischer Eleganz und technischer Effizienz. Als Hohlkugel mit konstanter Wandstärke vereint sie die natürliche Perfektion der Kugelform mit den Prinzipien intelligenter Materialnutzung. Ihre mathematischen Eigenschaften - mit den eleganten Differenz-Formeln für das Volumen und Summen-Formeln für die Oberfläche - machen sie zu einem fundamentalen Baustein moderner Ingenieurskunst. Von Hochdruck-Druckbehältern über Raumfahrttanks bis hin zu architektonischen Kuppelkonstruktionen zeigt die Kugelschale ihre universelle Anwendbarkeit. Sie demonstriert eindrucksvoll, wie geometrische Perfektion und praktische Materialeffizienz zu technischen Lösungen führen, die sowohl mathematisch schön als auch ingenieurstechnisch optimal sind.
|
|
|
|