Kugelecke Rechner
Rechner und Formeln zur Berechnung von Kugelecken
Kugelecke Rechner
Die Kugelecke
Die Kugelecke ist ein rechteckiger Ausschnitt aus einer Halbkugel mit charakteristischen geometrischen Eigenschaften.
Kugelecke Eigenschaften
Die Kugelecke: Rechteckiger Ausschnitt aus einer Halbkugel
Kugelecke Visualisierung
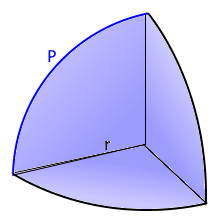
Die Kugelecke
Rechteckiger Ausschnitt aus einer Halbkugel
Spezielle Geometrie der Kugelecke.
Kombination aus geraden und gekrümmten Flächen.
|
|
Was ist eine Kugelecke?
Die Kugelecke ist ein spezieller geometrischer Körper:
- Definition: Rechteckiger Ausschnitt aus einer Halbkugel
- Form: Kombination aus geraden und gekrümmten Flächen
- Entstehung: Durch rechtwinklige Schnitte in der Halbkugel
- Anwendung: Architektur, Design, Engineering
- Besonderheit: Spezielle Oberflächenberechnung
- Geometrie: Einzigartige Volumen-/Flächenverhältnisse
Geometrische Eigenschaften der Kugelecke
Die Kugelecke zeigt einzigartige geometrische Eigenschaften:
Grundparameter
- Radius r: Grundlegender Bestimmungsparameter
- Bogenlänge P: Länge der gekrümmten Kanten
- Rechteckige Basis: Ebene Grundfläche
- Gekrümmte Oberfläche: Teil der ursprünglichen Kugel
Besondere Eigenschaften
- Hybride Form: Gerade und gekrümmte Flächen
- Spezielle Oberfläche: Faktor 5π/4 bei Oberflächenberechnung
- Einzigartiges Volumen: π/6 des Kugelradius³
- Architektonische Form: Häufig in modernem Design
Mathematische Beziehungen der Kugelecke
Die Kugelecke folgt speziellen mathematischen Gesetzen:
Volumen-Formel
Das Volumen ist ein Sechstel von π × r³. Deutlich kleiner als eine Halbkugel.
Oberflächen-Formel
Die Oberfläche mit Faktor 5π/4. Berücksichtigt gekrümmte und ebene Flächen.
Anwendungen der Kugelecke
Kugelecken finden Anwendung in verschiedenen Bereichen:
Architektur & Design
- Moderne Gebäudeecken
- Innenarchitektur (Nischen)
- Skulpturale Elemente
- Produktdesign
Ingenieurswesen
- Maschinenbau (Eckenverrundung)
- Werkzeugdesign
- Strömungstechnik
- Behältergeometrie
Kunst & Handwerk
- Bildhauerei
- Keramik und Töpferei
- Möbeldesign
- Schmuckherstellung
Mathematik & Geometrie
- Geometrische Studien
- Flächenberechnung
- Volumenoptimierung
- CAD-Anwendungen
Formeln zur Berechnung einer Kugelecke
Radius (r)
Radius aus verschiedenen Parametern
Bogenlänge (P)
Länge der gekrümmten Kanten
Oberfläche (S)
Gesamtoberfläche inklusive gekrümmter Teile
Volumen (V)
Ein Sechstel von π × r³
Berechnungsbeispiel für eine Kugelecke
Gegeben
Gesucht: Alle Parameter der Kugelecke
1. Bogenlängen-Berechnung
Für r = 12 cm:
\[P = \frac{r \cdot \pi}{2} = \frac{12 \cdot \pi}{2}\] \[P = 6\pi ≈ 18.85 \text{ cm}\]Die Bogenlänge beträgt etwa 18.85 cm
2. Oberflächen-Berechnung
Mit r = 12 cm:
\[S = \frac{5 \cdot \pi \cdot r^2}{4} = \frac{5 \cdot \pi \cdot 144}{4}\] \[S = \frac{720\pi}{4} = 180\pi\] \[S ≈ 565.49 \text{ cm}^2\]Die Oberfläche beträgt etwa 565.49 cm²
3. Volumen-Berechnung
Mit r = 12 cm:
\[V = \frac{\pi \cdot r^3}{6} = \frac{\pi \cdot 1728}{6}\] \[V = \frac{1728\pi}{6} = 288\pi\] \[V ≈ 904.78 \text{ cm}^3\]Das Volumen beträgt etwa 904.78 cm³
4. Zusammenfassung
Die Kugelecke mit Radius 12 cm
5. Vergleich mit anderen Körpern
V = 904.78 cm³
V = 3619.11 cm³
V = 7238.23 cm³
Die Kugelecke hat etwa 1/4 des Volumens einer Halbkugel
Die Kugelecke: Spezielle Geometrie zwischen Gerade und Kurve
Die Kugelecke ist ein faszinierender geometrischer Körper, der die Eleganz gekrümmter Flächen mit der Präzision rechteckiger Schnitte verbindet. Als rechteckiger Ausschnitt aus einer Halbkugel zeigt sie einzigartige mathematische Eigenschaften, die sie sowohl für theoretische Studien als auch für praktische Anwendungen interessant machen. Die Kugelecke verkörpert die perfekte Harmonie zwischen der natürlichen Rundung der Kugel und der konstruktiven Klarheit rechteckiger Geometrie.
Die Geometrie der Hybridform
Die Kugelecke zeigt die Faszination geometrischer Übergänge:
- Rechteckige Basis: Klare, ebene Grundfläche als Ausgangspunkt
- Gekrümmte Oberfläche: Erhalt der ursprünglichen Kugelkrümmung
- Spezielle Kanten: Übergang zwischen geraden und gekrümmten Bereichen
- Einzigartige Proportionen: Volumen π/6 r³, Oberfläche 5π/4 r²
- Mathematische Eleganz: Einfache Formeln trotz komplexer Geometrie
- Praktische Anwendbarkeit: Ideal für architektonische Lösungen
- Designpotential: Vielseitige ästhetische Möglichkeiten
Mathematische Besonderheiten
Formel-Spezialitäten
Die Kugelecke zeigt einzigartige Faktoren: 5π/4 für die Oberfläche und π/6 für das Volumen - mathematische Eleganz in spezieller Form.
Geometrische Übergänge
Die Verbindung von geraden und gekrümmten Flächen schafft interessante mathematische Herausforderungen in der Berechnung.
Praktische Relevanz
In Architektur und Design bietet die Kugelecke optimale Lösungen für Eckenverrundungen und ästhetische Übergänge.
Konstruktive Vorteile
Die Kombination aus rechteckiger Basis und gekrümmter Oberfläche ermöglicht sowohl konstruktive Klarheit als auch ästhetische Eleganz.
Zusammenfassung
Die Kugelecke verkörpert die perfekte Synthese zwischen geometrischer Klarheit und natürlicher Rundung. Als rechteckiger Ausschnitt aus einer Halbkugel verbindet sie die konstruktive Präzision rechteckiger Formen mit der ästhetischen Eleganz gekrümmter Oberflächen. Ihre speziellen mathematischen Eigenschaften - mit den charakteristischen Faktoren π/6 für das Volumen und 5π/4 für die Oberfläche - machen sie zu einem faszinierenden Studienobjekt der Geometrie. Von der modernen Architektur über Produktdesign bis hin zu ingenieurtechnischen Anwendungen bietet die Kugelecke vielseitige Lösungen für den Übergang zwischen geraden und gekrümmten Formen. Sie demonstriert eindrucksvoll, wie mathematische Präzision und ästhetische Schönheit in einer einzigen geometrischen Form harmonisch vereint werden können.
|
|
|
|