Riemenlänge berechnen

Rechner und Formeln zur Berechnung der Riemenlänge eines Antriebs

Riemenlänge Rechner

Riemenantrieb berechnen

Berechnet die Riemenlänge eines Antriebs mit zwei Riemenscheiben oder den Achsabstand, wenn die Länge des Riemens vorgegeben ist.

Riemenscheiben
Riemenantrieb mit zwei Scheiben
mm
mm
mm
Resultat
Riemenlänge:

Anwendungen

Praktische Anwendungen
Maschinenbau: Keilriemen, Flachriemen, Zahnriemen
Fahrzeugtechnik: Motorriemen, Nebenaggregateantrieb
Fördertechnik: Transportbänder, Förderbänder
Riementypen
  • Keilriemen: V-förmiger Querschnitt
  • Flachriemen: Rechteckiger Querschnitt
  • Zahnriemen: Mit Verzahnung
  • Rundriemen: Kreisförmiger Querschnitt
  • Polyriemen: Mehrfach-Keilriemen
  • Timing Belt: Synchronriemen

Formeln zur Riemenlänge

Die Riemenlänge berechnet sich aus der Geometrie der beiden Riemenscheiben und deren Abstand. Die exakte Formel berücksichtigt sowohl die geraden Abschnitte als auch die Umschlingungsbögen.

Exakte Riemenlängenformel

Präzise Berechnung für beliebige Scheibendurchmesser und Achsabstände.

\[L = (d_1 + d_2) \cdot \frac{\pi}{2} + (d_1 - d_2) \cdot \arcsin\left(\frac{d_1 - d_2}{2 \cdot D}\right) + 2 \cdot \sqrt{D^2 - 0{,}25 \cdot (d_1 - d_2)^2}\]
Diese Formel wird vom Rechner verwendet und ist für alle Konfigurationen genau.
Näherungsformel

Vereinfachte Berechnung für ähnliche Scheibendurchmesser.

\[L ≈ \frac{\pi}{2} \cdot (d_1 + d_2) + 2 \cdot D + \frac{(d_1 - d_2)^2}{4 \cdot D}\]
Gut für ähnliche Scheiben oder große Achsabstände.
Achsabstand berechnen

Umkehrung zur Berechnung des Achsabstands bei gegebener Riemenlänge.

\[D = \frac{b + \sqrt{b^2 - 32 \cdot (d_1 - d_2)^2}}{16}\] \[b = 4 \cdot L - 2 \cdot \pi \cdot (d_1 + d_2)\]
Für die Konstruktion mit vorgegebenem Riemen.
Symbole und Einheiten
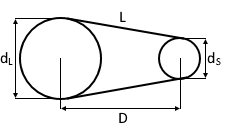
  • L = Riemenlänge
  • d₁ = Durchmesser der großen Scheibe
  • d₂ = Durchmesser der kleinen Scheibe
  • D = Achsabstand (Mittelpunkt zu Mittelpunkt)
  • Einheiten: Alle Maße in der gleichen Einheit
  • Hinweis: Durchmesser, nicht Radien verwenden
Beispiel: Keilriemenantrieb
Aufgabe:

Ein Keilriemenantrieb hat eine Antriebsscheibe mit 150 mm Durchmesser und eine Abtriebsscheibe mit 300 mm Durchmesser. Der Achsabstand beträgt 600 mm. Welche Riemenlänge wird benötigt?

Gegeben:
  • Durchmesser Scheibe 1: d₁ = 150 mm
  • Durchmesser Scheibe 2: d₂ = 300 mm
  • Achsabstand: D = 600 mm
  • Gesucht: Riemenlänge L
Lösung:
\[L = (d_1 + d_2) \cdot \frac{\pi}{2} + (d_1 - d_2) \cdot \arcsin\left(\frac{d_1 - d_2}{2 \cdot D}\right)\] \[+ 2 \cdot \sqrt{D^2 - 0{,}25 \cdot (d_1 - d_2)^2}\]
\[L = (150 + 300) \cdot \frac{\pi}{2} + (150 - 300) \cdot \arcsin\left(\frac{150 - 300}{2 \cdot 600}\right)\] \[+ 2 \cdot \sqrt{600^2 - 0{,}25 \cdot (150 - 300)^2}\]
\[L ≈ 707{,}1 + (-150) \cdot (-0{,}1253) + 2 \cdot 594{,}4\] \[L ≈ 707{,}1 + 18{,}8 + 1188{,}8 = 1914{,}7 \text{ mm}\]

Detaillierte Beschreibung der Riemenlängenberechnung

Physikalische Grundlagen

Diese Funktion berechnet die Riemenlänge eines Antriebs mit zwei Riemenscheiben oder den Abstand der Achsen, wenn die Länge des Riemens vorgegeben ist.

Bedienungshinweise

Zur Berechnung wählen Sie mit den Radiobuttons ob die Riemenlänge oder der Achsabstand berechnet werden soll. Dann tragen Sie die erforderlichen Werte ein und klicken den Button 'Rechnen'. Durchmesser, Abstände und Länge haben die gleiche Einheit (z.B. Meter oder cm).

Anwendungsbereiche

Maschinenbau

Keilriemen, Flachriemen, Zahnriemen, Industrieantriebe. Dimensionierung von Riemenantrieben und Übertragungssystemen.

Fahrzeugtechnik

Motorriemen, Nebenaggregateantrieb, Lichtmaschine, Wasserpumpe. Berechnung von Riemenlängen für Fahrzeugmotoren.

Fördertechnik

Transportbänder, Förderbänder, Bandantriebe. Auslegung von Förderanlagen und Transportsystemen.

Riemenantrieb verstehen

Ein Riemenantrieb überträgt Drehmoment durch Reibung zwischen Riemen und Scheiben. Die Geometrie bestimmt die erforderliche Riemenlänge:

Gerade Abschnitte

Trum 1: Oberer gerader Teil
Trum 2: Unterer gerader Teil
Länge: 2 × Tangentenlänge
Berechnung: Geometrisch

Umschlingungsbögen

Große Scheibe: Teilbogen
Kleine Scheibe: Größerer Bogen
Summe: < Vollkreis
Berechnung: Trigonometrisch

Gesamtlänge

L = Gerade Teile + Bögen
Exakt: Arcsin-Formel
Näherung: Für ähnliche Durchmesser
Anwendung: Je nach Genauigkeit

Wichtig: Die exakte Formel funktioniert gut für alle Scheibenverhältnisse. Die Näherungsformel versagt bei großen Durchmesserunterschieden und kleinen Achsabständen.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?


Weitere Physik Funktionen

Arbeit, Leistung und Zeit • Arbeit und Weg • Drehmoment • Druck, Kraft und Fläche • Gewichtskraft • Leistung, Kraft, Weg und Zeit • PS in kW umrechnen • PS in hp umrechnen • Schiefe Ebene • Wirkungsgrad • Zentrifugalkraft • Gravimetrische Energiedichte • Kinetische Energie • Volumetrische Energiedichte • Bahngeschwindigkeit • Beschleunigung nach Distanz • Beschleunigung nach Zeit • Geschwindigkeit, Weg und Zeit • Kreisbewegung • Winkelgeschwindigkeit • Fallgeschwindigkeit • Schalldruckpegel, Pacal und Dezibel • Schallgeschwindigkeit, Mach-Zahl • Schallgeschwindigkeit, Temperatur • Temperatur in der Atmosphäre • Getriebeübersetzung • Riemenlänge • Brechungswinkel