Spherical Segment Calculator
Online calculator and formulas for calculating parameters of a spherical segment
Spherical Segment Calculator
The Spherical Segment
The spherical segment is a part of a sphere that is cut out by two parallel planes.
Spherical Segment Properties
The spherical segment: Segment between two parallel planes
Spherical Segment Visualization
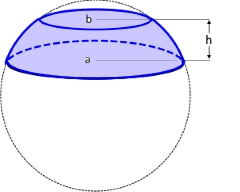
The Spherical Segment
Segment between two parallel planes
Complex geometry with curved zone.
Precise cutting by parallel planes.
What is a spherical segment?
The spherical segment is a special geometric shape:
- Definition: Part of a sphere between two parallel planes
- Sphere zone: The curved surface part of the segment
- Cutting circles: Circular edges with radii a and b
- Height h: Distance between the two cutting planes
- Application: Architecture, engineering, astronomy
- Feature: Complex calculation formulas due to geometry
Geometric properties of the spherical segment
The spherical segment shows complex geometric properties:
Basic parameters
- Radius a: Radius of the upper cutting circle
- Radius b: Radius of the lower cutting circle
- Height h: Distance between the parallel planes
- Sphere radius r: Radius of the original sphere
Special properties
- Sphere zone: Curved lateral surface between the circles
- Variable radii: a and b can be different sizes
- Complex formulas: Elaborate calculations due to geometry
- Position-dependent: Location in the original sphere relevant
Mathematical relationships of the spherical segment
The spherical segment follows complex mathematical laws:
Volume formula
The volume considers both radii and the height. Complex dependencies through cutting geometry.
Surface area formula
The surface area includes lateral and circular surfaces. Dependent on the sphere radius r.
Applications of the spherical segment
Spherical segments find applications in various fields:
Architecture & Construction
- Dome segments
- Vault calculations
- Modern architecture
- Bridge constructions
Geodesy & Astronomy
- Earth layer modeling
- Planetary segments
- Atmospheric layers
- Celestial sphere areas
Engineering
- Container segments
- Pipeline systems
- Mechanical engineering
- Fluid mechanics
Science & Research
- Physical models
- Materials science
- Biomechanics
- Crystallography
Formulas for the spherical segment
Sphere Radius (r)
Complex calculation from cutting parameters
Lateral Surface (M)
Curved surface of the sphere zone
Spherical Segment Surface (S)
Lateral surface plus both circular surfaces
Spherical Segment Volume (V)
Volume between the parallel planes
Distance to Upper Edge (dt)
Position of the segment in the sphere
Distance to Sphere Center (dm)
Average position of the segment
Calculation example for a spherical segment
Given
Find: All parameters of the spherical segment
1. Sphere radius calculation
For a = 6, b = 4, h = 2:
\[\frac{a^2 - b^2 - h^2}{2h} = \frac{36 - 16 - 4}{4} = 4\] \[r = \sqrt{36 + 16} = \sqrt{52} ≈ 7.21 \text{ cm}\]The sphere radius is approximately 7.21 cm
2. Lateral surface calculation
With r ≈ 7.21 cm, h = 2 cm:
\[M = 2 \cdot π \cdot r \cdot h\] \[M = 2 \cdot π \cdot 7.21 \cdot 2\] \[M ≈ 90.63 \text{ cm}^2\]The lateral surface is approximately 90.63 cm²
3. Total surface calculation
With the calculated values:
\[S = π \cdot (2rh + a^2 + b^2)\] \[S = π \cdot (28.84 + 36 + 16)\] \[S = π \cdot 80.84 ≈ 254.02 \text{ cm}^2\]The total surface is approximately 254.02 cm²
4. Volume calculation
With a = 6, b = 4, h = 2:
\[V = \frac{πh}{6} \cdot (3a^2 + 3b^2 + h^2)\] \[V = \frac{2π}{6} \cdot (108 + 48 + 4)\] \[V = \frac{π}{3} \cdot 160 ≈ 167.55 \text{ cm}^3\]The volume is approximately 167.55 cm³
5. Position determination
Distances in the sphere:
\[d_t = d_m = \frac{36 - 16 - 4}{4} = 4 \text{ cm}\]Distance to sphere center: 4 cm
The segment is located 4 cm from the sphere center
6. Summary
The spherical segment with a=6, b=4, h=2
7. Geometric analysis
a/b = 6/4 = 1.5
h/r = 2/7.21 ≈ 0.28
Outside center
Convex shape
The segment lies outside the sphere center with convex curvature
The Spherical Segment: Complex geometry between parallel planes
The spherical segment is a fascinating geometric shape that impressively demonstrates the complexity of three-dimensional cutting geometry. As part of a sphere that is cut out by two parallel planes, it combines curved and flat surface elements into a unique form. The mathematical challenge lies in the complex calculation formulas that must consider the position, orientation and size of the segment in the original sphere. The spherical segment shows how complex geometric relationships arise from simple cuts.
The geometry of parallel cuts
The spherical segment shows the fascination of geometric cutting operations:
- Parallel planes: Two parallel cutting planes define the segment
- Variable radii: Cutting circles with different radii a and b
- Sphere zone: The curved lateral surface between the circles
- Complex positioning: Location in the original sphere decisive
- Height dependency: Segment height h co-determines all properties
- Geometric reconstruction: Sphere radius calculable from segment parameters
- Diverse applications: From architecture to astronomy
Mathematical complexity
Reconstruction formulas
The calculation of the original sphere radius from the segment parameters shows the mathematical elegance of inverse geometry.
Position mathematics
The distance formulas enable precise localization of the segment within the original sphere.
Practical relevance
In architecture and engineering, spherical segments enable precise calculations of dome segments and vaulted structures.
Scientific application
In geodesy and astronomy, spherical segments help in modeling earth layers and atmospheric segments.
Summary
The spherical segment embodies the complexity and elegance of geometric cutting operations. As part of a sphere between two parallel planes, it shows how highly complex mathematical relationships arise from simple cuts. Its formulas - from the reconstruction of the original sphere radius through position determination to volume and surface calculations - demonstrate the power of analytical geometry. From architectural dome segments through geodetic earth layer modeling to astronomical applications, the spherical segment shows its universal significance. It connects the purity of geometric cuts with the practical necessity of complex calculations and remains a fundamental example of the beauty of mathematical geometry in three dimensions.