Spherical Wedge Calculator
Calculator and formulas for calculating a spherical wedge
Spherical Wedge Calculator
The Spherical Wedge
The spherical wedge is an angular section from a solid sphere, created by two half-planes.
Spherical Wedge Properties
The spherical wedge: Angle-dependent section from a solid sphere
Spherical Wedge Visualization
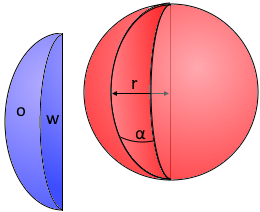
The Spherical Wedge
Angular section from a solid sphere
The spherical wedge with variable angle.
Bounded by two half-planes.
|
|
What is a spherical wedge?
The spherical wedge is a special geometric shape:
- Definition: Part of a solid sphere between two half-planes
- Boundary: Two half-planes with common diameter
- Surface: Spherical lune plus two half-circles
- Angle: Determines the size of the section
- Application: Geometry, architecture, mathematics
- Feature: Angle-proportional properties
Geometric properties of the spherical wedge
The spherical wedge shows angle-dependent geometric properties:
Basic parameters
- Radius r: Radius of the original sphere
- Angle α: Opening angle between the half-planes
- Half-planes: Two bounding surfaces through the center
- Spherical lune: Curved outer surface on the sphere
Special properties
- Angle proportionality: All properties proportional to α
- Symmetry: Mirror symmetric to angle bisector
- Completeness: At α = 360° results in solid sphere
- Wedge surface: Always π × r² independent of angle
Mathematical relationships of the spherical wedge
The spherical wedge follows angle-dependent mathematical laws:
Volume formula
The volume is directly proportional to angle α. Use angle in radians for calculation.
Outer surface formula
The outer surface (spherical lune) proportional to α. Curved surface on the sphere.
Applications of the spherical wedge
Spherical wedges find applications in various fields:
Geodesy & Cartography
- Time zone calculations
- Longitude and sectors
- Earth sphere division
- Geographic coordinates
Astronomy & Navigation
- Celestial sphere sectors
- Star coordinate systems
- Satellite navigation
- Planetary observation
Architecture & Design
- Dome segments
- Curved building parts
- Sculptural elements
- Industrial design
Mathematics & Physics
- Integral calculus
- Volume calculations
- Probability theory
- Geometric studies
Formulas for the spherical wedge
Volume (V)
Angle α in radians
Outer Surface (O)
Spherical lune - curved surface
Wedge Surface (W)
Constant - independent of angle
Total Surface (S)
Sum of outer and wedge surfaces
Angle conversion
\(α_{rad} = α_{deg} \cdot \frac{π}{180°}\)
\(α_{deg} = α_{rad} \cdot \frac{180°}{π}\)
\(360° = 2π \text{ rad}\)
Important: For calculations α must be in radians
Calculation example for a spherical wedge
Given
Find: All parameters of the spherical wedge
1. Angle conversion
Converting degrees to radians:
\[α = 60° \cdot \frac{π}{180°} = \frac{π}{3}\] \[α = \frac{π}{3} ≈ 1.047 \text{ rad}\]The angle is π/3 radians
2. Volume calculation
With α = π/3 and r = 6:
\[V = \frac{π}{3} \cdot \frac{2}{3} \cdot 6^3\] \[V = \frac{π}{3} \cdot \frac{2}{3} \cdot 216 = \frac{144π}{9} = 48π\] \[V ≈ 150.80 \text{ cm}^3\]The volume is approximately 150.80 cm³
3. Outer surface calculation
With α = π/3 and r = 6:
\[O = 2 \cdot \frac{π}{3} \cdot 6^2\] \[O = 2 \cdot \frac{π}{3} \cdot 36 = \frac{72π}{3} = 24π\] \[O ≈ 75.40 \text{ cm}^2\]The outer surface is approximately 75.40 cm²
4. Wedge surface calculation
With r = 6 (independent of angle):
\[W = π \cdot r^2 = π \cdot 6^2\] \[W = π \cdot 36 = 36π\] \[W ≈ 113.10 \text{ cm}^2\]The wedge surface is approximately 113.10 cm²
5. Total surface
Sum of outer and wedge surfaces:
\[S = O + W = 24π + 36π = 60π\] \[S ≈ 188.50 \text{ cm}^2\]The total surface is approximately 188.50 cm²
6. Summary
The spherical wedge with 60° opening angle
7. Proportion of solid sphere
V = 150.80 cm³
V = 904.78 cm³
60°/360° = 1/6
The 60° spherical wedge has 1/6 the volume of the solid sphere
The Spherical Wedge: Angular geometry of the sphere
The spherical wedge is a fascinating geometric shape that combines the elegance of sphere geometry with the precision of angle-based calculations. As an angular section from a solid sphere, bounded by two half-planes through the center, it shows the perfect proportionality between angle and geometric properties. The spherical wedge embodies the mathematical beauty of angle-dependent geometry and finds wide application in geodesy, astronomy and architecture.
The geometry of angles
The spherical wedge shows the fascination of angle-dependent geometry:
- Half-plane boundaries: Two half-planes through a common diameter
- Spherical lune: Curved outer surface on the original sphere surface
- Angle proportionality: Volume and outer surface directly proportional to angle
- Constant wedge surface: π × r² independent of opening angle
- Symmetry: Mirror symmetric to angle bisector
- Scalability: Continuously defined from 0° to 360°
- Universal application: From time zones to celestial sphere sectors
Mathematical elegance
Proportionality laws
The elegant proportionality between angle and volume (α × 2/3 × r³) and outer surface (2α × r²) shows the mathematical purity of the spherical wedge.
Angular geometry
The use of radians enables direct proportionality and elegant formulas without complicated conversion factors.
Practical relevance
From time zone calculations to astronomical coordinates to architectural dome segments - the spherical wedge is omnipresent.
Geodetic significance
In geodesy, the spherical wedge enables precise calculations of earth sphere sectors, longitudes and geographic coordinates.
Summary
The spherical wedge embodies the perfect harmony between angular geometry and sphere volume. As an angular section from a solid sphere, it shows the elegant proportionality of mathematical laws - volume and outer surface are directly proportional to the opening angle, while the wedge surface remains constant. This mathematical clarity makes it an indispensable tool in geodesy, astronomy and navigation. From the division of the earth sphere into time zones to the calculation of celestial sphere sectors to architectural applications in dome constructions - the spherical wedge connects theoretical angular geometry with practical solutions. It impressively demonstrates how simple geometric principles become powerful mathematical tools that shape our world from the smallest angle measurement to the largest geodetic calculation.
|
|
|
|