Ellipsoid Volumen Rechner
Rechner und Formeln zur präzisen Berechnung des Volumens eines Ellipsoids
Ellipsoid Volumen Rechner
Das Ellipsoid-Volumen
Das Ellipsoid-Volumen wird durch eine elegante Formel mit drei Halbachsen a, b und c berechnet.
Ellipsoid Volumen Eigenschaften
Die Volumenformel: Elegant und universell anwendbar
Ellipsoid Visualisierung
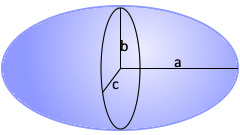
Das Ellipsoid mit drei Halbachsen.
Volumen einfach berechenbar.
|
|
Was ist das Ellipsoid-Volumen?
Das Ellipsoid-Volumen ist ein fundamentales geometrisches Maß:
- Definition: Rauminhalt des dreidimensionalen Ellipsoids
- Formel: Einfache Multiplikation der drei Halbachsen
- Universalität: Gilt für alle Ellipsoid-Typen
- Präzision: Exakte mathematische Berechnung
- Anwendung: Von Molekülen bis zu Planeten
- Eleganz: Schöne Verallgemeinerung der Kugelformel
Geometrische Grundlagen des Ellipsoid-Volumens
Das Ellipsoid-Volumen basiert auf fundamentalen geometrischen Prinzipien:
Volumen-Grundlagen
- Drei Halbachsen: a, b, c bestimmen die Form
- Symmetrie: Mittelpunktsymmetrischer Körper
- Skalierung: Linear mit jeder Achse
- π-Faktor: Verbindung zur Kreisgeometrie
Besondere Eigenschaften
- Kugelverallgemeinerung: Kugel als Spezialfall (a=b=c)
- Dimensionsanalyse: Kubische Einheiten
- Proportionalität: Verdopplung einer Achse → doppeltes Volumen
- Universalität: Gleiche Formel für alle Ellipsoid-Typen
Mathematische Aspekte der Volumenberechnung
Die Ellipsoid-Volumenformel zeigt mathematische Eleganz:
Formel-Struktur
Elegante Verallgemeinerung der Kugelformel. Exakt und einfach zu berechnen.
Mathematische Eigenschaften
Dreifachintegral über Ellipsoid-Bereich. Koordinatentransformation zu Kugel.
Anwendungen der Ellipsoid-Volumenberechnung
Ellipsoid-Volumenberechnungen finden vielfältige Anwendung:
Naturwissenschaften
- Zellvolumen in der Biologie
- Molekülvolumen in der Chemie
- Partikelvolumen in der Physik
- Tropfenvolumen in der Strömungslehre
Astronomie & Geophysik
- Planetenvolumen
- Asteroidenvolumen
- Erdellipsoid-Berechnungen
- Satellitenbahnanalyse
Ingenieurswesen
- Behältervolumen
- Materialmengen-Berechnung
- CAD-Volumenbestimmung
- Fertigungsplanung
Medizin & Biologie
- Organvolumen
- Tumorvolumen
- Zellgrößenanalyse
- Medizinische Bildgebung
Die Ellipsoid-Volumenformel
Volumen (V) - Hauptformel
Die universelle Formel für jedes Ellipsoid
Spezialfall: Kugel (a = b = c = r)
Die bekannte Kugelformel als Spezialfall
Rotationsellipsoid (b = c)
Vereinfachung für rotationssymmetrische Formen
Dimensionsanalyse
Volumen hat immer kubische Längeneinheiten
Herleitung durch Integration
Transformation des Ellipsoids zur Einheitskugel durch Koordinatensubstitution
Berechnungsbeispiel für das Ellipsoid-Volumen
Gegeben
Gesucht: Volumen des Ellipsoids mit drei verschiedenen Halbachsen
Schritt-für-Schritt Berechnung
1. Formel einsetzen:
\[V = \frac{4}{3} \cdot \pi \cdot a \cdot b \cdot c\]2. Werte einsetzen:
\[V = \frac{4}{3} \cdot \pi \cdot 8 \cdot 6 \cdot 4\]3. Berechnen:
\[V = \frac{4}{3} \cdot \pi \cdot 192 = 256\pi\]4. Numerisches Ergebnis:
\[V ≈ 804.25 \text{ cm}^3\]Das Ellipsoid hat ein Volumen von etwa 804.25 cm³
Ergebnis-Analyse
Vergleich mit Kugel:
Äquivalente Kugel:
\(r = \sqrt[3]{\frac{abc \cdot 4}{4}} = \sqrt[3]{192} ≈ 5.77 \text{ cm}\)
Das Ellipsoid entspricht einer Kugel mit Radius ≈ 5.77 cm
Beispiel: Kugel
\(V = \frac{4}{3}\pi \cdot 5^3 = \frac{500\pi}{3} ≈ 523.6 \text{ cm}^3\)
Beispiel: Prolat
\(V = \frac{4}{3}\pi \cdot 10 \cdot 3^2 = 120\pi ≈ 377.0 \text{ cm}^3\)
Beispiel: Oblat
\(V = \frac{4}{3}\pi \cdot 3 \cdot 7^2 = 196\pi ≈ 615.8 \text{ cm}^3\)
Das Ellipsoid-Volumen: Eleganz der dreidimensionalen Geometrie
Das Ellipsoid-Volumen repräsentiert eine der elegantesten Formeln der dreidimensionalen Geometrie. Mit ihrer einfachen Struktur V = (4/3)πabc verallgemeinert sie die klassische Kugelformel auf beliebige ellipsoidale Formen und ermöglicht präzise Volumenberechnungen für eine Vielzahl natürlicher und technischer Objekte. Von biologischen Zellen über Planetenkörper bis hin zu industriellen Behältern - die Ellipsoid-Volumenformel ist ein universelles Werkzeug der angewandten Mathematik.
Die mathematische Schönheit der Volumenformel
Das Ellipsoid-Volumen zeigt die Eleganz der analytischen Geometrie:
- Universelle Gültigkeit: Eine Formel für alle Ellipsoid-Typen
- Lineare Skalierung: Verdopplung einer Achse verdoppelt das Volumen
- Symmetrische Struktur: Alle drei Halbachsen gleichberechtigt
- π-Verbindung: Elegante Verbindung zur Kreisgeometrie
- Integral-Herleitung: Rigorose mathematische Fundierung
- Dimensionale Konsistenz: Kubische Einheiten als natürliches Ergebnis
- Grenzwert-Verhalten: Natürlicher Übergang zu Kugel und Zylindern
Praktische Bedeutung und Anwendungen
Wissenschaftliche Präzision
Die exakte Volumenformel ermöglicht präzise Berechnungen in Naturwissenschaft und Technik, von der Molekularchemie bis zur Astronomie.
Universelle Anwendbarkeit
Von der kleinsten biologischen Zelle bis zum größten Planeten - die Ellipsoid-Volumenformel beschreibt Objekte aller Größenklassen.
Ingenieurtechnische Relevanz
In der Technik ermöglicht die Formel präzise Materialberechnungen, Fertigungsplanung und Qualitätskontrolle ellipsoidaler Bauteile.
Bildungsrelevanz
Als Verallgemeinerung der Kugelformel vermittelt sie tiefes Verständnis für dreidimensionale Geometrie und Integralrechnung.
Zusammenfassung
Die Ellipsoid-Volumenformel V = (4/3)πabc verkörpert mathematische Eleganz in ihrer reinsten Form. Ihre einfache Struktur verbirgt die tiefe geometrische Einsicht, dass das Volumen eines beliebigen Ellipsoids durch das Produkt seiner drei Halbachsen und dem universellen Faktor (4/3)π bestimmt wird. Diese Formel verbindet theoretische Schönheit mit praktischer Anwendbarkeit und zeigt, wie die Mathematik komplexe dreidimensionale Formen mit elementaren Operationen beschreibt. Von der Grundlagenforschung bis zur industriellen Anwendung bleibt das Ellipsoid-Volumen ein fundamentales Werkzeug der angewandten Geometrie, das die Brücke zwischen abstrakter Mathematik und konkreter Realität schlägt.
|
|
|
|