Rechteck in Quadrat umrechnen
Rechner für flächengleiche Quadrat-Rechteck Transformationen
Quadrat ⇄ Rechteck Umrechner
Flächengleiche Transformation
Umwandlung zwischen Rechteck und Quadrat mit identischem Flächeninhalt durch geometrische Optimierung.
Quadrat ⇄ Rechteck Vergleich
Transformation Eigenschaften
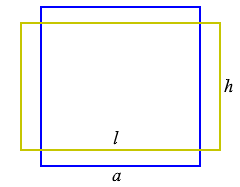
Prinzip: Gleiche Fläche A, verschiedene Umfänge und Proportionen
Quadrat und Rechteck mit gleicher Fläche.
Das Quadrat hat den minimalen Umfang.
|
|
Quadrat-Rechteck Transformation: Die Kunst der flächengleichen Umwandlung
Die Transformation zwischen Quadrat und Rechteck bei gleichem Flächeninhalt zeigt fundamentale Prinzipien der Geometrie:
- Flächengleichheit: A□ = A▭ = konstant
- Quadratwurzel-Beziehung: a = √(l × h)
- Umfang-Optimierung: Quadrat hat minimalen Umfang
- Proportions-Wandel: Von 1:1 zu l:h Verhältnis
- Isoperimetrisches Problem: Optimale Flächen-Umfang-Relation
- Geometrische Effizienz: Quadrat als optimale Form
Geometrische Prinzipien der Flächenumwandlung
Die mathematischen Beziehungen zwischen flächengleichen Quadraten und Rechtecken:
Flächenerhaltung
- Quadrat: A = a²
- Rechteck: A = l × h
- Gleichheit: a² = l × h
- Transformation: a = √(l × h)
Umfang-Unterschiede
- Quadrat: P□ = 4a = 4√(l × h)
- Rechteck: P▭ = 2(l + h)
- Minimaler Umfang beim Quadrat
- Isoperimetrisches Optimum
Mathematik der Flächentransformation
Die algebraischen Beziehungen ermöglichen elegante Umrechnungen:
Quadratwurzel-Beziehungen
- a = √A (aus Fläche)
- a = √(l × h) (aus Rechteck)
- h = A/l = a²/l (Höhe berechnen)
- l = A/h = a²/h (Länge berechnen)
Optimierungs-Prinzipien
- Minimaler Umfang bei gegebener Fläche
- Geometrisches vs. arithmetisches Mittel
- Lagrange-Multiplikatoren
- Variationsrechnung Grundlagen
Anwendungen der Quadrat-Rechteck Transformation
Flächenumwandlungen haben vielfältige praktische Bedeutungen:
Architektur & Raumplanung
- Grundriss-Optimierung gleicher Fläche
- Energieeffiziente Gebäude-Proportionen
- Material-Effizienz bei Außenwänden
- Raumaufteilung und Möblierung
Produktion & Fertigung
- Materialzuschnitt-Optimierung
- Verpackungs-Design und -Effizienz
- Logistik und Lagerplatz-Planung
- Produktions-Layout-Optimierung
Digital & Interface Design
- Responsive Layout-Design
- Bildschirm-Optimierung verschiedener Formate
- UI-Element Proportionen
- Print vs. Digital Format-Anpassungen
Natur & Umwelt
- Landschafts-Gestaltung und -Planung
- Garten-Design mit optimaler Flächennutzung
- Biologische Habitat-Optimierung
- Ökosystem-Design und Biodiversität
Formeln für Quadrat ⇄ Rechteck Transformation
Quadrat-Seitenlänge a
Geometrisches Mittel der Rechteck-Seiten
Rechteck-Dimensionen
Umkehrbeziehungen für Rechteck-Seiten
Flächeninhalt A
Flächengleichheit als Grundprinzip
Umfang-Beziehungen
Verschiedene Umfänge bei gleicher Fläche
Umfang-Optimierung
Quadrat hat minimalen Umfang bei gegebener Fläche
Geometrisches Mittel
Geometrisches ≤ Arithmetisches Mittel
Rechenbeispiel für Quadrat-Rechteck Transformation
Gegeben
Gesucht: Alle Parameter des flächengleichen Quadrats und Rechtecks
1. Rechteck vervollständigen
Höhe aus Fläche und Länge, dann Umfang
2. Quadrat berechnen
Seitenlänge aus Fläche, dann Umfang
3. Transformation bestätigen
Quadratwurzel-Beziehung und geometrisches Mittel bestätigt
4. Vollständige Transformation
Gleiche Fläche, Quadrat hat 20% weniger Umfang!
Die Quadrat-Rechteck Transformation: Optimierung in der Geometrie
Die Transformation zwischen Quadrat und Rechteck bei konstanter Fläche verkörpert fundamentale Prinzipien der geometrischen Optimierung. Diese scheinbar einfache Umwandlung enthüllt tiefe mathematische Wahrheiten über Effizienz, das geometrische Mittel und das berühmte isoperimetrische Problem. Von der Antike bis zur modernen Architektur beeinflusst diese Transformation unser Verständnis optimaler Formen.
Das isoperimetrische Problem und seine Lösung
Die Quadrat-Rechteck Transformation illustriert einen Spezialfall des isoperimetrischen Problems:
- Umfang-Minimierung: Bei gegebener Fläche hat das Quadrat den kleinsten Umfang
- Geometrisches Mittel: a = √(l×h) - fundamentale Beziehung zwischen den Dimensionen
- AM-GM Ungleichung: √(l×h) ≤ (l+h)/2 mit Gleichheit nur bei l = h (Quadrat)
- Variationsrechnung: Mathematischer Beweis der Optimalität des Quadrats
- Lagrange-Multiplikatoren: Eleganter Optimierungsansatz für Nebenbedingungen
- Perimeter-Effizienz: Quadrat ist die "sparsamste" rechteckige Form
Historische Entwicklung und kulturelle Bedeutung
Die Erkenntnis der Quadrat-Optimierung hat eine lange Geschichte:
Antike Mathematik
Bereits die alten Griechen erkannten, dass das Quadrat bei gegebener Fläche den minimalen Umfang hat. Euklid behandelte verwandte Probleme in seinen "Elementen".
Mittelalterliche Geometrie
Islamische Mathematiker entwickelten algebraische Methoden zur Flächenumwandlung. Diese beeinflussten später die Renaissance-Architektur.
Moderne Analysis
Euler und die Bernoullis formalisierten die Variationsrechnung, wodurch die Optimalität des Quadrats mathematisch beweisbar wurde.
Zeitgenössische Anwendung
Heute nutzen Architekten und Designer diese Prinzipien für energieeffiziente Gebäude und materialoptimierte Konstruktionen.
Praktische Auswirkungen in Technik und Design
Die Quadrat-Rechteck Transformation hat weitreichende praktische Konsequenzen:
- Energieeffiziente Architektur: Quadratische Grundrisse minimieren Wärmeverluste
- Materialoptimierung: Weniger Außenwand-Material bei gleichem Wohnraum
- Produktionseffizienz: Optimaler Zuschnitt rechteckiger Materialien
- Logistik-Optimierung: Beste Raumausnutzung in quadratischen Containern
- Urban Planning: Quadratische Stadtblöcke für optimale Infrastruktur
- Display Technology: Quadratische Pixel für effiziente Bildschirm-Layouts
Mathematische Tiefe und Verbindungen
Die Transformation offenbart tiefe mathematische Zusammenhänge:
Geometrische Mittel
Das geometrische Mittel √(l×h) ist immer kleiner oder gleich dem arithmetischen Mittel (l+h)/2. Diese Ungleichung erklärt die Umfang-Effizienz des Quadrats.
Optimierungstheorie
Die Quadrat-Transformation ist ein Paradebeispiel für Optimierung mit Nebenbedingungen. Lagrange-Multiplikatoren führen elegant zur Lösung.
Differentialgeometrie
Die Krümmung der "Iso-Flächen-Kurven" im Parameterraum (l,h) erklärt geometrisch, warum das Quadrat optimal ist.
Funktionalanalysis
Das Problem kann als Minimierung eines Funktionals im Hilbert-Raum formuliert werden - ein Tor zur modernen Analysis.
Zukunftsperspektiven und moderne Anwendungen
Die Prinzipien der Quadrat-Rechteck Transformation bleiben hochrelevant:
- Sustainable Architecture: Klimaneutrale Gebäude nutzen optimale Grundriss-Proportionen
- AI-optimierte Layouts: Machine Learning findet optimale Raum-Aufteilungen
- 3D-Printing: Materialeffiziente Strukturen durch geometrische Optimierung
- Nano-Engineering: Optimale Formen für molekulare Maschinen
- Space Habitats: Raumstationen nutzen optimale Geometrien für Lebensraum
- Virtual Reality: Optimierte virtuelle Räume für immersive Erfahrungen
Zusammenfassung
Die Quadrat-Rechteck Transformation verkörpert die Essenz geometrischer Optimierung. Diese elegante mathematische Beziehung - a = √(l×h) - verbindet das geometrische Mittel mit dem isoperimetrischen Problem und zeigt, wie das Quadrat bei gegebener Fläche den minimalen Umfang erzielt. Von antiken griechischen Erkenntnissen über moderne Variationsrechnung bis zu zeitgenössischen Anwendungen in nachhaltiger Architektur und KI-optimiertem Design bleibt diese fundamentale Transformation ein Eckpfeiler effizienter Gestaltung. Sie erinnert uns daran, dass in der scheinbaren Einfachheit des Quadrats eine tiefe mathematische Wahrheit liegt - die perfekte Balance zwischen Form und Funktion, zwischen Ästhetik und Effizienz.
|
|
|
|