Kugelsegment Rechner
Rechner und Formeln zur Berechnung eines Kugelsegments (Kugelabschnitt, Kugelkappe)
Kugelsegment Rechner
Das Kugelsegment
Das Kugelsegment ist ein durch einen Schnitt abgetrennter Teil einer Kugel mit kuppelförmiger Gestalt.
Kugelsegment Eigenschaften
Das Kugelsegment: Kuppelförmiger Teil einer Kugel
Kugelsegment Visualisierung
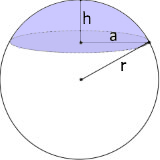
Das Kugelsegment
Kuppelförmiger Kugelabschnitt
Klassische Kuppelgeometrie.
Basis für Architektur und Design.
|
|
Was ist ein Kugelsegment?
Das Kugelsegment ist ein grundlegender geometrischer Körper:
- Definition: Durch einen Schnitt abgetrennter Teil einer Kugel
- Form: Kuppelförmige Gestalt mit ebener Grundfläche
- Kugelkappe: Der gekrümmte Teil der Oberfläche
- Sonderfall: Halbkugel ist ein spezielles Kugelsegment
- Anwendung: Architektur, Kuppelbauten, Design
- Besonderheit: Kombiniert gekrümmte und ebene Flächen
Geometrische Eigenschaften des Kugelsegments
Das Kugelsegment zeigt charakteristische geometrische Eigenschaften:
Grundparameter
- Kugelradius r: Radius der ursprünglichen Vollkugel
- Segmenthöhe h: Höhe des kuppelförmigen Abschnitts
- Segmentradius a: Radius der kreisförmigen Grundfläche
- Schnittebene: Definiert die Abtrennungsposition
Besondere Eigenschaften
- Kuppelform: Natürliche, stabile Bauform
- Hybride Oberfläche: Gekrümmte Kappe plus ebene Basis
- Skalierbarkeit: Von flachem Segment bis zur Halbkugel
- Symmetrie: Rotationssymmetrisch um die Mittelachse
Mathematische Beziehungen des Kugelsegments
Das Kugelsegment folgt eleganten mathematischen Gesetzen:
Volumen-Formel
Das Volumen wächst quadratisch mit der Höhe. Berücksichtigt die Krümmung der ursprünglichen Kugel.
Oberflächen-Formel
Die Oberfläche setzt sich aus gekrümmter Kappe und ebener Grundfläche zusammen.
Anwendungen des Kugelsegments
Kugelsegmente finden Anwendung in verschiedenen Bereichen:
Architektur & Bau
- Kuppel-Konstruktionen
- Kirchen und Moscheen
- Moderne Architektur
- Planetarien
Ingenieurswesen
- Druckbehälter-Böden
- Tankdeckel
- Rohrleitungs-Kappen
- Maschinenbau
Design & Kunst
- Produktdesign
- Skulpturale Elemente
- Möbeldesign
- Dekorative Objekte
Wissenschaft & Natur
- Geodäsie
- Optik (Linsen)
- Biologie (Zellformen)
- Astronomie
Formeln zum Kugelsegment
Segment Volumen (Vs)
Volumen des kuppelförmigen Segments
Segment Höhe (h)
Höhe aus Kugel- und Segmentradius
Segment Radius (a)
Radius der kreisförmigen Grundfläche
Oberfläche der Kappe (Sc)
Gekrümmte Oberfläche der Kugelkappe
Segment Basisfläche (A)
Kreisförmige Grundfläche des Segments
Segment Oberfläche (S)
Kappe plus Grundfläche
Berechnungsbeispiel für ein Kugelsegment
Gegeben
Gesucht: Alle Parameter des Kugelsegments
1. Segmentradius-Berechnung
Für r = 10 cm, h = 4 cm:
\[a = \sqrt{r^2 - (r - h)^2}\] \[a = \sqrt{100 - (10 - 4)^2}\] \[a = \sqrt{100 - 36} = \sqrt{64} = 8 \text{ cm}\]Der Segmentradius beträgt 8 cm
2. Volumen-Berechnung
Mit r = 10 cm, h = 4 cm:
\[V_s = \frac{π \cdot h^2}{3} \cdot (3r - h)\] \[V_s = \frac{π \cdot 16}{3} \cdot (30 - 4)\] \[V_s = \frac{16π \cdot 26}{3} ≈ 435.6 \text{ cm}^3\]Das Segmentvolumen beträgt etwa 435.6 cm³
3. Basisflächen-Berechnung
Mit a = 8 cm:
\[A = π \cdot a^2 = π \cdot 64\] \[A ≈ 201.06 \text{ cm}^2\]Die Basisfläche beträgt etwa 201.06 cm²
4. Kappenoberflächen-Berechnung
Mit r = 10 cm, h = 4 cm:
\[S_c = 2πrh = 2π \cdot 10 \cdot 4\] \[S_c = 80π ≈ 251.33 \text{ cm}^2\]Die Kappenoberfläche beträgt etwa 251.33 cm²
5. Gesamtoberflächen-Berechnung
Kappe plus Basis:
\[S = S_c + A\] \[S = 251.33 + 201.06\] \[S ≈ 452.39 \text{ cm}^2\]Die Gesamtoberfläche beträgt etwa 452.39 cm²
6. Zusammenfassung
Das Kugelsegment mit 4 cm Höhe
7. Vergleich mit Halbkugel
V = 435.6 cm³
V = 2094.4 cm³
≈ 20.8%
Das Segment hat etwa 1/5 des Volumens einer Halbkugel
8. Geometrische Analyse
h/r = 4/10 = 0.4
a/r = 8/10 = 0.8
Flache Kappe
Schwach gekrümmt
Bei h/r = 0.4 entsteht eine relativ flache Kugelkappe
Das Kugelsegment: Klassische Kuppelgeometrie
Das Kugelsegment ist einer der fundamentalsten und ästhetisch ansprechendsten geometrischen Körper der Mathematik. Als kuppelförmiger Abschnitt einer Kugel vereint es die natürliche Eleganz sphärischer Krümmung mit der praktischen Funktionalität einer ebenen Grundfläche. Seine mathematischen Eigenschaften - von der quadratischen Höhenabhängigkeit des Volumens bis zur linearen Beziehung zwischen Kappenoberfläche und Höhe - machen es zu einem idealen Beispiel für die Schönheit geometrischer Zusammenhänge. Das Kugelsegment ist die Grundlage unzähliger architektonischer Meisterwerke und technischer Lösungen.
Die Geometrie der Kuppel
Das Kugelsegment zeigt die Perfektion kuppelförmiger Geometrie:
- Kuppelform: Natürlich stabile und ästhetisch ansprechende Form
- Ebene Grundfläche: Praktische Aufstandsfläche für Konstruktionen
- Kugelkappe: Gekrümmte Oberfläche mit optimaler Spannungsverteilung
- Skalierbare Geometrie: Von flacher Kappe bis zur Halbkugel
- Rotationssymmetrie: Perfekte Symmetrie um die vertikale Achse
- Mathematische Eleganz: Einfache Beziehungen zwischen Parametern
- Universelle Anwendung: Von Architektur bis Ingenieurtechnik
Mathematische Schönheit
Volumen-Eleganz
Die Volumenformel V = πh²(3r-h)/3 zeigt die quadratische Abhängigkeit von der Höhe und die elegante Berücksichtigung der Kugelkrümmung.
Oberflächen-Harmonie
Die Kappenoberfläche S = 2πrh ist linear zur Höhe proportional, was zu harmonischen Größenverhältnissen führt.
Architektonische Perfektion
Kuppeln aus Kugelsegmenten bieten optimale Statik, natürliche Akustik und zeitlose ästhetische Wirkung.
Technische Exzellenz
In der Technik ermöglichen Kugelsegmente optimale Druckverteilung in Behältern und Rohrleitungen.
Zusammenfassung
Das Kugelsegment verkörpert die perfekte Synthese zwischen mathematischer Eleganz und praktischer Funktionalität. Als kuppelförmiger Abschnitt einer Kugel zeigt es die natürliche Schönheit gekrümmter Geometrie und die konstruktive Klarheit ebener Grundflächen. Seine mathematischen Eigenschaften - von der quadratischen Höhenabhängigkeit des Volumens bis zur linearen Kappenoberfläche - demonstrieren die harmonischen Beziehungen der sphärischen Geometrie. Von den majestätischen Kuppeln historischer Bauwerke über moderne architektonische Meisterwerke bis hin zu technischen Anwendungen in Maschinenbau und Verfahrenstechnik zeigt das Kugelsegment seine universelle Bedeutung. Es verbindet die Reinheit geometrischer Formen mit der Funktionalität praktischer Anwendungen und bleibt ein zeitloses Symbol für die Einheit von Schönheit und Zweckmäßigkeit in der Geometrie.
|
|
|
|