Calculate Airy Function
Online calculator and formulas for computing the Airy functions Ai(x) and Bi(x)
Airy Function Calculator
Airy Functions
The Airy functions Ai(x) and Bi(x) are special functions for solving linear differential equations y'' - xy = 0.
Airy Function Curves
Mouse pointer on the graph shows the values
|
|
Airy Function Formulas
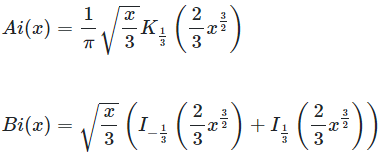
Description
The Airy function is a special mathematical function that frequently appears in physics and optics. It is named after the British astronomer George Biddell Airy, who used it in his work on optics.
Properties
- Ai(z): Airy function of the first kind
- Bi(z): Airy function of the second kind
- Solutions to the Airy equation
- Applications in quantum mechanics
Detailed Description of the Airy Function
Mathematical Foundations
The Airy functions \(\displaystyle Ai (x) \) and the related function \(\displaystyle Bi(x)\) denote a special function in mathematics for solving the linear differential equation \(\displaystyle y'' -xy=0\).
Calculation Instructions
To calculate, enter the argument, then click the 'Calculate' button.
The Airy function here expects a real number as argument. The Airy function for complex numbers can be found in the complex numbers section.
Applications
Ai(z) - First Kind
The Airy function of the first kind is a solution to the Airy equation, also called the Stokes equation. It appears in optics, quantum mechanics, electromagnetism, and radiation transfer.
Bi(z) - Second Kind
The Airy function of the second kind is another solution to the Airy equation. It is linearly independent of Ai(z) and is also used in various physical contexts.
Quantum Mechanics
The Airy functions are closely related to the solution of the Schrödinger equation for a linear potential well. Their properties, zeros, and asymptotic behavior are of particular interest.
|
|
|
|