Airy Funktion berechnen
Online Rechner und Formeln zur Berechnung der Airy Funktionen Ai(x) und Bi(x)
Airy Funktion Rechner
Airy Funktionen
Die Airy Funktionen Ai(x) und Bi(x) sind spezielle Funktionen zur Lösung linearer Differentialgleichungen y'' - xy = 0.
Airy Funktionskurven
Mauszeiger auf der Grafik zeigt die Werte an
|
|
Formeln zu den Airy Funktionen
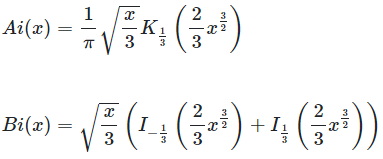
Beschreibung
Die Airy-Funktion ist eine spezielle mathematische Funktion, die in der Physik und Optik häufig vorkommt. Sie ist nach dem britischen Astronomen George Biddell Airy benannt, der sie in seinen Arbeiten zur Optik verwendete.
Eigenschaften
- Ai(z): Airy-Funktion erster Art
- Bi(z): Airy-Funktion zweiter Art
- Lösungen der Airy-Gleichung
- Anwendung in Quantenmechanik
Detaillierte Beschreibung der Airy Funktion
Mathematische Grundlagen
Die Airy Funktionen \(\displaystyle Ai (x) \) und die verwandte Funktion \(\displaystyle Bi(x)\) bezeichnen eine spezielle Funktion in der Mathematik zur Lösungen der linearen Differentialgleichung \(\displaystyle y'' -xy=0\).
Hinweise zur Berechnung
Zur Berechnung geben Sie das Argument ein, dann klicken Sie auf den Button 'Rechnen'.
Die Airy Funktion hier erwartet als Argument eine reelle Zahl. Die Airy Funktion für komplexe Zahlen finden Sie im Bereich der komplexen Zahlen.
Anwendungsbereiche
Ai(z) - Erste Art
Die Airy-Funktion erster Art ist eine Lösung der Airy-Gleichung oder auch Stokes-Gleichung genannt. Sie tritt in der Optik, Quantenmechanik, Elektromagnetik und Strahlungsübertragung auf.
Bi(z) - Zweite Art
Die Airy-Funktion zweiter Art ist eine weitere Lösung der Airy-Gleichung. Sie ist linear unabhängig von Ai(z) und wird ebenfalls in verschiedenen physikalischen Kontexten verwendet.
Quantenmechanik
Die Airy-Funktionen sind eng mit der Lösung der Schrödinger-Gleichung für einen linearen Potentialtopf verbunden. Ihre Eigenschaften, Nullstellen und asymptotisches Verhalten sind von besonderem Interesse.
|
|
|
|