Calculate Bessel-I Function

Online calculator for the modified Bessel function Iᵥ(z) of the first kind - Exponential behavior for heat conduction and waveguides

Bessel-I Function Calculator

Modified Bessel Function

The Iᵥ(z) or modified Bessel function shows exponential behavior instead of oscillation and is important for cylindrical symmetry.

Order number (integer)
Function argument (z > 0)
Result
Iᵥ(z):

Bessel-I Function Curve

Mouse pointer on the graph shows the values.
The modified Bessel function shows exponential growth.

Why exponential instead of oscillatory behavior?

The modified Bessel function differs fundamentally from the ordinary Bessel function:

  • Exponential growth: Iᵥ(z) grows exponentially for large z
  • No oscillation: No periodic up and down behavior
  • Physical relevance: Describes diffusion and heat conduction
  • Cylindrical symmetry: Important for cylindrical coordinates
  • Monotonicity: Strictly monotonically increasing for z > 0
  • Asymptotics: Iᵥ(z) ~ e^z/√(2πz) for large z

Applications in cylindrical systems

The modified Bessel function is fundamental for problems with cylindrical symmetry:

Heat Conduction
  • Temperature distribution in cylinders
  • Heat conduction in pipelines
  • Cooling/heating of cylindrical objects
Electromagnetics
  • Waveguides (coaxial cables)
  • Electromagnetic fields
  • Antenna theory

Formulas for the Bessel-I Function

Definition via J-Function
\[I_\nu(z) = i^{-\nu} J_\nu(iz)\]

Relationship to ordinary Bessel function

Recurrence Formula
\[I_{\nu-1}(z) - I_{\nu+1}(z) = \frac{2\nu}{z} I_\nu(z)\]

Relationship between different orders

Series Expansion
\[I_\nu(z) = \sum_{k=0}^{\infty} \frac{1}{k! \Gamma(k+\nu+1)} \left(\frac{z}{2}\right)^{2k+\nu}\]

Power series expansion

Integral Representation
\[I_n(z) = \frac{1}{\pi} \int_0^\pi e^{z \cos \theta} \cos(n\theta) d\theta\]

For integer order n

Asymptotic Form
\[I_\nu(z) \sim \frac{e^z}{\sqrt{2\pi z}} \left(1 - \frac{4\nu^2-1}{8z} + \ldots\right)\]

For large z

Special Values

Important Values
I₀(0) = 1 I₁(0) = 0 I₀(1) ≈ 1.266
Symmetry Properties
I_{-n}(z) = I_n(z)

For integer n

Behavior at z = 0
\[I_\nu(0) = \begin{cases} 1 & \text{if } \nu = 0 \\ 0 & \text{if } \nu > 0 \end{cases}\]

Limiting behavior at origin

Application Areas

Heat conduction, electromagnetic waveguides, diffusion processes, statistical mechanics.

Wronskian Determinant
\[W[I_\nu, K_\nu] = -\frac{1}{z}\]

With K-function (second kind)

Comparison of Bessel Functions

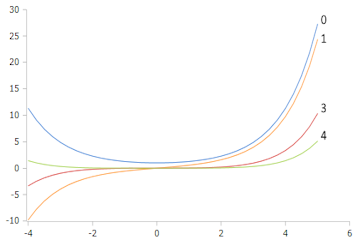
Bessel-I Functions
Bessel-I Functions (Order 0,1,3,4)

All show exponential growth for large z values. Higher orders start flatter but also grow exponentially.

Characteristic Properties
  • I₀(z) starts at 1 and grows monotonically
  • Iₙ(z) with n > 0 starts at 0
  • All functions are strictly convex
  • Asymptotically: ~ e^z/√(2πz)

Detailed Description of the Bessel-I Function

Mathematical Definition

The modified Bessel function of the first kind Iᵥ(z) is a fundamental solution of the modified Bessel differential equation. Unlike the ordinary Bessel function, it shows exponential growth instead of oscillatory behavior.

Definition: Iᵥ(z) = i^(-ν) Jᵥ(iz)
Using the Calculator

Enter the order ν (integer) and the argument z (positive real number). For negative z, the result may become complex.

Historical Background

The modified Bessel functions were developed by Friedrich Bessel (1784-1846) and later systematized by Lord Kelvin and others for physical applications. The name "modified" refers to the transformation iz → z.

Properties and Applications

Physical Applications
  • Heat conduction in cylindrical objects
  • Electromagnetic waveguides
  • Diffusion processes with cylindrical symmetry
  • Membrane vibrations
Mathematical Properties
  • Exponential growth for large z
  • Strict monotonicity for z > 0
  • Symmetry: I₋ₙ(z) = Iₙ(z) for integer n
  • Convexity for all real z > 0
Numerical Aspects
  • Stability: Numerically stable for z ≥ 0
  • Scaling: Exponential growth requires caution
  • Recursion: Efficient computation via recurrence formulas
  • Asymptotics: Asymptotic expansions for large z
Interesting Facts
  • Function I₀(z) describes the probability density of the von Mises distribution
  • For very small z: Iᵥ(z) ≈ (z/2)^ν / Γ(ν+1)
  • The functions satisfy the modified Bessel differential equation
  • Important in quantum field theory and statistical mechanics

Calculation Examples

Example 1

I₀(1) ≈ 1.266

Bessel-I zeroth order at z = 1

Example 2

I₁(2) ≈ 1.591

Bessel-I first order at z = 2

Example 3

I₂(3) ≈ 2.245

Bessel-I second order at z = 3

Bessel Functions Classification

Bessel of the First Kind (Jᵥ)

Solutions of the standard Bessel equation:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Oscillatory behavior, finite at z = 0 for ν ≥ 0.

Bessel of the Second Kind (Yᵥ)

Also called Neumann functions:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Singular at z = 0, oscillating for large z.

Modified Bessel (Iᵥ, Kᵥ)

Exponential behavior:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\] \[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]

Iᵥ: exponentially growing, Kᵥ: exponentially decaying.

Differential Equation and Solution Theory

Modified Bessel Equation
\[z^2 \frac{d^2y}{dz^2} + z \frac{dy}{dz} - (z^2 + \nu^2)y = 0\]

The modified Bessel equation with parameter ν.

General Solution
\[y(z) = C_1 I_\nu(z) + C_2 K_\nu(z)\]

Linear combination of the two linearly independent solutions.

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?


More special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta