Calculate Derivative Softsign Function

Online calculator for computing the derivative of the Softsign function - Gentle gradient function for neural networks

Softsign Derivative Calculator

Softsign Derivative

The softsign'(x) or Softsign derivative is a gentle gradient function for stable training of neural networks.

Any real number (-∞ to +∞)
Result
softsign'(x):

Gentle Bell-shaped Curve

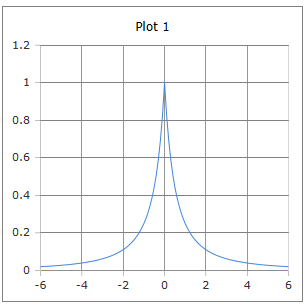
Softsign Derivative Curve

Curve of the derivative Softsign function: Gentle bell curve with maximum at x = 0.
Properties: Maximum 1 at x = 0, always positive, slower decline than Sigmoid.

Why is the Softsign derivative gentler?

The gentle bell shape of the Softsign derivative offers advantages for training neural networks:

  • Slower decline: Less abrupt gradient changes
  • Always positive: No negative gradients
  • Symmetry: Uniform shape left and right
  • Gentle saturation: Fewer vanishing gradients
  • Computationally efficient: Simple calculation
  • Stability: Better numerical properties

Gentle gradients for stable training

The simple form softsign'(x) = 1/(1+|x|)² makes computation efficient and stable:

\[\frac{\partial L}{\partial w} = \frac{\partial L}{\partial \text{softsign}} \cdot \text{softsign}'(x) \cdot \frac{\partial x}{\partial w}\]

The gentle derivative leads to more uniform gradient flows and more stable convergence compared to other activation functions.

Softsign Derivative Formulas

Basic Formula
\[\text{softsign}'(x) = \frac{1}{(1+|x|)^2}\]

Simple rational function

Symmetry
\[\text{softsign}'(-x) = \text{softsign}'(x)\]

Even function

Piecewise Form
\[\text{softsign}'(x) = \begin{cases} \frac{1}{(1+x)^2} & \text{if } x \geq 0 \\ \frac{1}{(1-x)^2} & \text{if } x < 0 \end{cases}\]

Split representation

Chain Rule Form
\[\frac{d}{dx}\text{softsign}(f(x)) = \text{softsign}'(f(x)) \cdot f'(x)\]

For composite functions

Maximum Property
\[\max(\text{softsign}'(x)) = \text{softsign}'(0) = 1\]

Maximum at x = 0

Properties

Special Values
softsign'(0) = 1 softsign'(1) = 0.25 softsign'(±∞) = 0
Domain
x ∈ (-∞, +∞)

All real numbers

Range
\[\text{softsign}'(x) \in (0, 1]\]

Between 0 and 1

Application

Backpropagation, gentle gradients, stable training, alternative to Sigmoid derivative.

Asymptotic Behavior
\[\lim_{x \to \pm\infty} \text{softsign}'(x) = 0\]

Approaches 0 for large |x|

Detailed Description of the Softsign Derivative

Mathematical Definition

The derivative of the Softsign function is a gentle, bell-shaped function that plays an important role in training neural networks. It offers a computationally efficient alternative to other activation derivatives.

Definition: softsign'(x) = 1/(1+|x|)²
Using the Calculator

Enter any real number and click 'Calculate'. The derivative is defined for all real numbers and has values between 0 and 1.

Historical Background

The Softsign derivative evolved as part of the search for better gradient functions for neural networks. It was proposed as a gentle alternative to steeper derivatives like the Sigmoid derivative.

Properties and Applications

Machine Learning Applications
  • Backpropagation in neural networks
  • Gentle gradient computation
  • More stable training than steep derivatives
  • Alternative to Sigmoid derivative
Computational Advantages
  • Simple rational function
  • No exponential functions required
  • Numerically stable for all inputs
  • Lower computational cost than Sigmoid derivative
Mathematical Properties
  • Maximum: softsign'(0) = 1 at x = 0
  • Symmetry: softsign'(-x) = softsign'(x)
  • Monotonicity: Monotonically decreasing for |x| > 0
  • Positivity: Always positive
Interesting Facts
  • The simple form makes backpropagation very efficient
  • Maximum of 1 at x = 0 means strongest learning rate at center
  • Gentler decline than Sigmoid derivative reduces vanishing gradients
  • Always positive values avoid sign-switching problems

Calculation Examples

Example 1

softsign'(0) = 1

Maximum of derivative → Strongest learning rate

Example 2

softsign'(1) = 0.25

Medium input → Moderate learning rate

Example 3

softsign'(3) ≈ 0.063

Large input → Gentle damping

Comparison with Other Derivatives

vs. Sigmoid Derivative

Softsign' vs. σ'(x) = σ(x)(1-σ(x)):

  • Higher maximum (1 vs. 0.25)
  • Gentler decline for large |x|
  • Simpler calculation
  • Fewer vanishing gradients
vs. Tanh Derivative

Softsign' vs. 1 - tanh²(x):

  • Same maximum of 1
  • Slower saturation
  • No exponential functions
  • Better numerical stability

Advantages and Disadvantages

Advantages
  • Simple, efficient calculation
  • Higher maximum than Sigmoid derivative
  • Gentler gradient decline
  • Always positive values
  • Numerically stable
  • Fewer vanishing gradients
Disadvantages
  • Less widespread than Sigmoid/Tanh derivatives
  • Can still saturate in very large networks
  • Slower than ReLU (constant derivative)
  • Limited empirical studies
  • Not as aggressive as modern activations

Impact on Training

Gradient Flow

The gentle form leads to more stable gradients:

\[\frac{\partial L}{\partial w_i} = \frac{\partial L}{\partial a} \cdot \frac{1}{(1+|z|)^2} \cdot x_i\]

More uniform weight updates through gentle derivative.

Convergence

Properties of convergence:

  • More stable convergence than steep derivatives
  • Fewer oscillations in training
  • More uniform learning rate over time
  • More robust to hyperparameter choices


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree