Calculate Derivative Sigmoid Function
Online calculator for computing the derivative of the Sigmoid function - Essential for backpropagation in neural networks
Sigmoid Derivative Calculator
Sigmoid Derivative
The σ'(x) or Sigmoid derivative is essential for Gradient Descent and backpropagation in neural networks.
Bell-shaped Derivative Curve
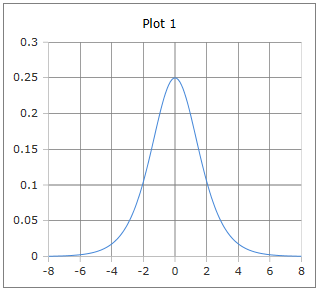
The curve of the derivative sigmoid function: Bell-shaped curve with maximum at x = 0.
Properties: Maximum 0.25 at x = 0, symmetric, approaches 0 for large |x|.
Why is the Sigmoid derivative bell-shaped?
The bell-shaped curve of the Sigmoid derivative has special properties for machine learning:
- Maximum at x = 0: Greatest rate of change at the center
- Symmetry: Same shape left and right
- Bounded values: Between 0 and 0.25
- Vanishing gradients: Approaches 0 for large |x|
- Backpropagation: Determines learning speed
- Optimization: Important for gradient descent
Chain Rule and Backpropagation
The elegant form σ'(x) = σ(x)(1-σ(x)) makes computation in neural networks particularly efficient:
Since σ(x) has already been computed, σ'(x) requires only a simple multiplication, making backpropagation very efficient.
Sigmoid Derivative Formulas
Elegant Form
Expressed through the Sigmoid function itself
Exponential Form
Direct derivative of the exponential form
Chain Rule Form
For composite functions
Alternative Form
With positive exponential function
Tanh Representation
Hyperbolic secant function
Maximum Property
Maximum at x = 0
Properties
Special Values
Domain
All real numbers
Range
Between 0 and 0.25
Application
Backpropagation, Gradient Descent, neural network optimization, Deep Learning.
Detailed Description of the Sigmoid Derivative
Mathematical Definition
The derivative of the Sigmoid function is one of the most elegant mathematical formulas in Machine Learning. It shows how the Sigmoid function changes at each point and is fundamental for training neural networks through backpropagation.
Using the Calculator
Enter any real number and click 'Calculate'. The derivative is defined for all real numbers and has values between 0 and 0.25.
Historical Background
This elegant derivative formula was first systematically used in the 1980s by Rumelhart, Hinton, and Williams for backpropagation. It revolutionized the training of multi-layer neural networks.
Properties and Applications
Machine Learning Applications
- Backpropagation in neural networks
- Gradient descent optimization
- Error backpropagation in deep learning
- Adaptive learning rate algorithms
Numerical Properties
- Computational efficiency (uses already computed σ(x))
- Numerical stability for large |x|
- Smooth, differentiable function
- Bounded values prevent explosions
Mathematical Properties
- Maximum: σ'(0) = 0.25 at x = 0
- Symmetry: σ'(-x) = σ'(x)
- Convexity: Concave for |x| < ln(2+√3)
- Asymptotic: Exponential decay for large |x|
Interesting Facts
- The elegant form σ'(x) = σ(x)(1-σ(x)) makes backpropagation efficient
- The maximum 0.25 at x = 0 determines maximum learning speed
- Vanishing gradients problem: σ'(x) → 0 for large |x|
- Foundation for modern activation functions like ReLU
Calculation Examples
Example 1
σ'(0) = 0.25
Maximum of derivative → Best learning rate
Example 2
σ'(2) ≈ 0.105
Positive input → Medium learning rate
Example 3
σ'(5) ≈ 0.007
Large input → Slow learning
Role in Backpropagation
Gradient Calculation
In backpropagation, the Sigmoid derivative is used for the chain rule:
Where δⱼ is the error of neuron j and wⱼₖ are the weights.
Weight Update
The weights are updated proportional to the derivative:
Where η is the learning rate and E is the error function.
Vanishing Gradients Problem
Problem
For large |x|, σ'(x) becomes very small, leading to slow learning:
- σ'(5) ≈ 0.007 (very slow)
- σ'(10) ≈ 0.00005 (practically stopped)
- Deep networks particularly affected
Solution Approaches
Modern approaches to solve the problem:
- ReLU activation functions
- Residual connections (ResNet)
- Batch normalization
- LSTM/GRU for sequences
|
|