Logit Function

Online calculator and formulas for the Logit function - inverse function of the Sigmoid function for Machine Learning

Logit Function Calculator

Logit (Log-Odds) Function

The logit(p) or Log-Odds function is the inverse function of the Sigmoid function and central in Machine Learning.

Probability value between 0 and 1 (exclusive)
Result
logit(p):

Logit Function Curve

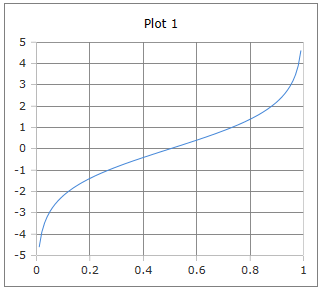
Logit Curve

Logit Function Curve: The function maps probabilities (0,1) to real numbers (-∞,+∞).
Properties: Strictly monotonically increasing, symmetric around (0.5, 0).

Logit Function Formulas

Basic Formula
\[\text{logit}(p) = \ln\left(\frac{p}{1-p}\right)\]

Logarithm of the odds (odds ratio)

Alternative Form
\[\text{logit}(p) = -\ln\left(\frac{1}{p}-1\right)\]

Equivalent representation

Arctanh Form
\[\text{logit}(p) = 2 \cdot \text{arctanh}(2p-1)\]

Hyperbolic representation

Inverse Function
\[\text{sigmoid}(x) = \frac{1}{1+e^{-x}}\]

Sigmoid as inverse of the Logit function

Logistic Regression
\[\text{logit}(p) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_k x_k\]

Linear combination of predictors in logit space

Properties

Special Values
logit(0.5) = 0 logit(0.25) ≈ -1.1 logit(0.75) ≈ 1.1
Domain
p ∈ (0, 1)

Open between 0 and 1 (exclusive)

Range
\[\text{logit}(p) \in (-\infty, +\infty)\]

All real numbers

Application

Machine Learning, logistic regression, statistics and data analysis.

What are Odds (Odds Ratio)?

Odds describe the ratio of the probability for an event to the probability against the event:

\[\text{Odds} = \frac{p}{1-p} = \frac{\text{Probability for}}{\text{Probability against}}\]

Example: With a probability of 75% (p = 0.75):

  • Odds = 0.75 / 0.25 = 3
  • Interpretation: "3 to 1" or "3:1"
  • Log-Odds = ln(3) ≈ 1.099

Advantages of Log-Odds:

  • Symmetric around 0
  • Unlimited range
  • Linear in regression models

Detailed Description of the Logit Function

Mathematical Definition

The Logit function is the inverse function of the Sigmoid function and transforms probabilities (0,1) into the entire real number range (-∞,+∞). It is the heart of logistic regression and many Machine Learning algorithms.

Definition: logit(p) = ln(p/(1-p))
Using the Calculator

Enter a probability between 0 and 1 (exclusive) and click 'Calculate'. The function is not defined for p = 0 or p = 1.

Historical Background

The Logit function was introduced in the 1940s by Joseph Berkson as an alternative to probit analysis. The name "Logit" is a contraction of "Logistic Unit" and quickly became the standard in statistics.

Properties and Applications

Machine Learning Applications
  • Logistic regression (binary classification)
  • Neural networks (activation function)
  • Generalized linear models (GLM)
  • Bayesian statistics and MCMC
Statistical Applications
  • Epidemiology (disease risk)
  • Econometrics (voting behavior)
  • Psychometrics (Item Response Theory)
  • Bioinformatics (gene expression)
Special Properties
  • Monotonicity: Strictly monotonically increasing
  • Symmetry: logit(p) = -logit(1-p)
  • Linearity: Enables linear modeling
  • Interpretability: Coefficients as log-odds
Interesting Facts
  • The Logit function is the canonical link function for the binomial distribution
  • It transforms bounded probabilities into unbounded log-odds
  • Central to maximum likelihood estimation in logistic regression
  • Related to the logistic growth model in population dynamics

Calculation Examples

Example 1

logit(0.5) = 0

Neutral probability → Log-Odds = 0

Example 2

logit(0.75) ≈ 1.099

75% probability → Odds 3:1

Example 3

logit(0.25) ≈ -1.099

25% probability → Odds 1:3

Logistic Regression

Model Equation

In logistic regression, the logit transformation is used:

\[\text{logit}(p) = \beta_0 + \beta_1 x_1 + \ldots + \beta_k x_k\]

This enables linear modeling of probabilities.

Interpretation

The coefficients βᵢ have a clear interpretation:

  • exp(βᵢ): Odds Ratio
  • βᵢ > 0: Increases the odds
  • βᵢ < 0: Decreases the odds
  • βᵢ = 0: No effect

Is this page helpful?            
Thank you for your feedback!

Sorry about that

How can we improve it?


IT Functions

Decimal, Hex, Bin, Octal conversion • Shift bits left or right • Set a bit • Clear a bit • Bitwise AND • Bitwise OR • Bitwise exclusive OR

Special functions

Airy • Derivative Airy • Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye • Spherical-Bessel-J • Spherical-Bessel-Y • Hankel • Beta • Incomplete Beta • Incomplete Inverse Beta • Binomial Coefficient • Binomial Coefficient Logarithm • Erf • Erfc • Erfi • Erfci • Fibonacci • Fibonacci Tabelle • Gamma • Inverse Gamma • Log Gamma • Digamma • Trigamma • Logit • Sigmoid • Derivative Sigmoid • Softsign • Derivative Softsign • Softmax • Struve • Struve table • Modified Struve • Modified Struve table • Riemann Zeta

Hyperbolic functions

ACosh • ACoth • ACsch • ASech • ASinh • ATanh • Cosh • Coth • Csch • Sech • Sinh • Tanh

Trigonometrische Funktionen

ACos • ACot • ACsc • ASec • ASin • ATan • Cos • Cot • Csc • Sec • Sin • Sinc • Tan • Degree to Radian • Radian to Degree