Calculate Softsign Function
Online calculator and formulas for the Softsign function - Alternative to Tanh activation function in neural networks
Softsign Function Calculator
Softsign Activation Function
The softsign(x) or Softsign function is a smooth alternative to the Tanh function as an activation function in neural networks.
|
|
Smooth S-shaped Curve
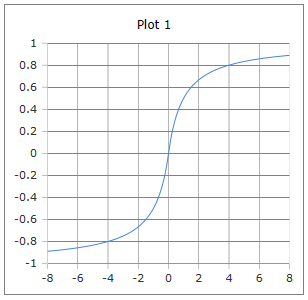
The curve of the Softsign function: Smooth S-shape with values between -1 and +1.
Properties: Smooth, monotonically increasing, slower saturation than Tanh.
Why is Softsign a smooth alternative?
The Softsign function offers several advantages over other activation functions:
- Slow saturation: Less aggressive asymptotes than Tanh
- Simple calculation: Only division and absolute value
- Symmetry: Point symmetric around the origin
- Bounded output: Values between -1 and +1
- Zero-centered: Output centered around 0
- Monotonicity: Strictly monotonically increasing
Comparison: Softsign vs. Tanh
Both functions have S-shaped curves with values between -1 and +1, but different characteristics:
Softsign: x/(1+|x|)
- Slow saturation for large |x|
- Computationally less expensive
- Linear behavior around x = 0
- Less vanishing gradients
Tanh: (e^x - e^(-x))/(e^x + e^(-x))
- Fast saturation for large |x|
- Exponential functions required
- S-shaped behavior around x = 0
- Stronger vanishing gradients
Softsign Function Formulas
Basic Formula
Simple rational function
Derivative
Always positive
Piecewise Definition
Split representation
Inverse Function
For |y| < 1
Limits
Horizontal asymptotes
Symmetry
Odd function
Properties
Special Values
Domain
All real numbers
Range
Between -1 and +1
Application
Neural networks, Deep Learning, alternative activation function, smooth normalization.
Detailed Description of the Softsign Function
Mathematical Definition
The Softsign function is a smooth, S-shaped function developed as an alternative to the hyperbolic tangent function. It offers similar properties to Tanh but is computationally cheaper and shows different saturation behavior.
Using the Calculator
Enter any real number and click 'Calculate'. The function is defined for all real numbers and returns values between -1 and +1.
Historical Background
The Softsign function was developed as part of the search for better activation functions for neural networks. It was particularly proposed in the early 2000s as a computationally efficient alternative to Tanh.
Properties and Applications
Machine Learning Applications
- Activation function in neural networks
- Alternative to Tanh in hidden layers
- Smooth normalization of input values
- Regularization through slower saturation
Computational Advantages
- No exponential functions required
- Simple derivative for backpropagation
- Numerically stable for all input values
- Lower computational cost than Tanh
Mathematical Properties
- Monotonicity: Strictly monotonically increasing
- Symmetry: Odd function (point symmetric)
- Differentiability: Differentiable everywhere except at x = 0
- Saturation: Slow approach to ±1
Interesting Facts
- The derivative softsign'(x) = 1/(1+|x|)² is always positive
- Softsign saturates slower than Tanh, meaning fewer vanishing gradients
- The function is not differentiable at x = 0 (but continuous)
- Computational cost is significantly lower than Sigmoid or Tanh
Calculation Examples
Example 1
softsign(0) = 0
Neutral input → Zero output
Example 2
softsign(1) = 0.5
Positive input → Positive activation
Example 3
softsign(-3) = -0.75
Negative input → Negative activation
Comparison with Other Activation Functions
vs. Tanh
Softsign vs. hyperbolic tangent:
- Similar range (-1, 1)
- Slower saturation
- Lower computational costs
- Fewer vanishing gradients
vs. Sigmoid
Softsign vs. Sigmoid function:
- Symmetric around zero (vs. 0-1 range)
- Zero-centered output
- Better convergence properties
- Simpler calculation
vs. ReLU
Softsign vs. Rectified Linear Unit:
- Bounded output (vs. unbounded)
- Smooth function (vs. non-differentiable)
- Active in both directions
- More complex calculation
Advantages and Disadvantages
Advantages
- Computationally efficient (no exponential functions)
- Zero-centered output improves convergence
- Slower saturation reduces vanishing gradients
- Numerically stable for all input values
- Simple implementation
Disadvantages
- Not differentiable at x = 0 (practically often negligible)
- Slower than ReLU-based functions
- Less widespread than Sigmoid/Tanh
- Can still saturate in very large networks
- Limited empirical studies compared to ReLU
|
|
|
|