Zehneck (Dekagon) berechnen

Rechner und Formeln für regelmäßige Zehnecke

Dekagon Rechner

Regelmäßiges Zehneck

Ein regelmäßiges Dekagon hat 10 gleich lange Seiten und 10 gleich große Winkel (144°). Es zeigt eine enge Verbindung zum goldenen Schnitt.

Bekannten Parameter eingeben
Welcher Parameter ist bekannt?
Wert des ausgewählten Parameters
Berechnungsergebnisse
Seitenlänge a:
Umfang P:
Fläche A:
Höhe h:
Diagonale d5:
Diagonale d4:
Diagonale d3:
Diagonale d2:
Innenradius ri:
Außenradius ra:

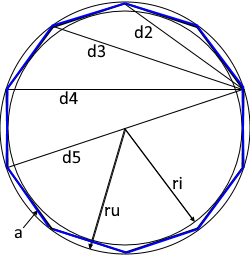
Regelmäßiges Dekagon

Das Diagramm zeigt ein regelmäßiges Zehneck mit allen relevanten Parametern.
Alle Seiten sind gleich lang, alle Innenwinkel betragen 144°.

Dekagon

Eigenschaften eines regelmäßigen Zehnecks

Ein regelmäßiges Zehneck (Dekagon) ist ein faszinierendes geometrisches Objekt:

  • 10 gleiche Seiten: Alle Seitenlängen sind identisch
  • 10 gleiche Winkel: Jeder Innenwinkel beträgt exakt 144°
  • Winkelsumme: 8 × 180° = 1440°
  • Goldener Schnitt: Enge Verbindung zu φ = 1,618...
  • Symmetrie: 10-fache Rotationssymmetrie
  • Konstruierbarkeit: Mit Zirkel und Lineal konstruierbar

Der goldene Schnitt im Dekagon

Das regelmäßige Zehneck zeigt eine besondere Beziehung zum goldenen Schnitt:

Goldenes Verhältnis φ
\[\varphi = \frac{1 + \sqrt{5}}{2} \approx 1.618\]

Der goldene Schnitt erscheint in vielen Formeln des Dekagons

Umkreisradius
\[r_a = \varphi \cdot a\]

Der Umkreisradius ist das φ-fache der Seitenlänge

Konstruktion und mathematische Besonderheiten

Das regelmäßige Zehneck ist ein besonders interessantes Polygon:

Klassische Konstruktion
  • Mit Zirkel und Lineal konstruierbar
  • Über den goldenen Schnitt aufbaubar
  • Durch Halbierung des Fünfecks erstellbar
  • Zentrumswinkel: 360°/10 = 36°
Mathematische Eigenschaften
  • Trigonometrische Werte sind algebraisch
  • cos(36°) und sin(36°) haben geschlossene Form
  • Verbindung zu Fibonacci-Zahlen
  • Fünfeck-Symmetrie als Grundlage

Anwendungen des regelmäßigen Zehnecks

Regelmäßige Zehnecke finden in verschiedenen Bereichen Anwendung:

Münzwesen & Medaillen
  • Sondermünzen mit Zehneck-Form
  • Gedenkmedaillen und Auszeichnungen
  • Sammlerprägungen
  • Historische Münzformen
Kunst & Design
  • Architektonische Grundrisse
  • Rosettenfenster in Kirchen
  • Dekorative Ornamente
  • Moderne Designobjekte
Wissenschaft & Technik
  • Kristallographie und Molekularstrukturen
  • Antennentechnik für Rundstrahlung
  • Optische Systeme
  • Rotationssymmetrische Bauteile
Spiele & Unterhaltung
  • Gesellschaftsspiele mit Zehneck-Feldern
  • Puzzle und Legespiele
  • Geometrische Rätsel
  • Bildungsmedien für Mathematik

Formeln für das regelmäßige Zehneck (Dekagon)

Flächeninhalt A
\[A = \frac{5}{2} \sqrt{5 + 2\sqrt{5}} \cdot a^2 \approx 7.694 \cdot a^2\]

Komplexe Formel mit Verschachtelten Wurzeln

Umfang P
\[P = 10 \cdot a\]

Einfach: 10-mal die Seitenlänge

Diagonale d₂
\[d_2 = \frac{1}{2}\sqrt{10 + 2\sqrt{5}} \cdot a \approx 1.902 \cdot a\]

Kürzeste Diagonale

Diagonale d₃
\[d_3 = \frac{1}{2}\sqrt{14 + 6\sqrt{5}} \cdot a \approx 2.618 \cdot a\]

Mittlere Diagonale

Diagonale d₄ (Höhe h)
\[d_4 = h = \sqrt{5 + 2\sqrt{5}} \cdot a \approx 3.078 \cdot a\]

Längste Diagonale = Höhe

Diagonale d₅
\[d_5 = (1 + \sqrt{5}) \cdot a \approx 3.236 \cdot a\]

Maximale Diagonale mit goldenem Schnitt

Umkreisradius rₐ
\[r_a = \frac{1 + \sqrt{5}}{2} \cdot a \approx 1.618 \cdot a = \varphi \cdot a\]

Goldener Schnitt mal Seitenlänge

Innenkreisradius rᵢ
\[r_i = \frac{1}{2}\sqrt{5 + 2\sqrt{5}} \cdot a \approx 1.539 \cdot a\]

Radius des einbeschriebenen Kreises

Rechenbeispiel für ein Dekagon

Gegeben
Seitenlänge a = 4

Gesucht: Alle Eigenschaften des regelmäßigen Zehnecks

1. Grundmaße berechnen
\[P = 10 \times 4 = 40\] \[A = 7.694 \times 16 = 123.11\]

Umfang und Flächeninhalt

2. Radien berechnen
\[r_a = 1.618 \times 4 = 6.47\] \[r_i = 1.539 \times 4 = 6.16\]

Umkreis- und Innenkreisradius

3. Alle Diagonalen
d₂ = 1.902 × 4 = 7.61 d₃ = 2.618 × 4 = 10.47
d₄ = h = 3.078 × 4 = 12.31 d₅ = 3.236 × 4 = 12.94

Alle vier verschiedenen Diagonallängen

4. Vollständige Zusammenfassung
Seitenlänge a = 4.00 Umfang P = 40.00 Fläche A = 123.11 Höhe h = 12.31
Umkreisradius = 6.47 Innenkreisradius = 6.16 Innenwinkel = 144° Zentrumswinkel = 36°

Komplette Charakterisierung des regelmäßigen Zehnecks

Das regelmäßige Zehneck in Mathematik und Natur

Das regelmäßige Zehneck nimmt eine besondere Stellung unter den regelmäßigen Polygonen ein. Seine enge Verbindung zum goldenen Schnitt und zu den Eigenschaften des regulären Fünfecks macht es zu einem mathematisch faszinierenden Objekt mit überraschend vielen praktischen Anwendungen.

Mathematische Tiefe und goldener Schnitt

Die mathematischen Eigenschaften des regelmäßigen Zehnecks zeigen eine bemerkenswerte Tiefe:

  • Goldener Schnitt φ: Erscheint in nahezu allen wichtigen Formeln (φ = (1+√5)/2 ≈ 1.618)
  • Algebraische Wurzeln: Alle trigonometrischen Werte sind in geschlossener Form darstellbar
  • Konstruierbarkeit: Mit Zirkel und Lineal konstruierbar (Gauß'sches Kriterium erfüllt)
  • Pentagonale Symmetrie: Basiert auf der 5-fachen Rotationssymmetrie des Fünfecks
  • Diophantische Eigenschaften: Verbindungen zu zahlentheoretischen Problemen

Konstruktion und geometrische Eleganz

Die Konstruktion des regelmäßigen Zehnecks offenbart geometrische Eleganz:

Klassische Methoden

Konstruktion über den goldenen Schnitt, durch Halbierung eines regulären Fünfecks oder über die Teilung eines Kreises in zehn gleiche Teile mittels des 36°-Winkels.

Moderne Ansätze

Koordinatengeometrie, trigonometrische Methoden und algorithmische Konstruktion in CAD-Systemen nutzen die algebraischen Eigenschaften.

Symmetrieeigenschaften

10-fache Rotationssymmetrie, 10 Spiegelachsen und Verbindung zur Symmetriegruppe D₁₀ machen es zu einem perfekten Beispiel für diskrete Symmetrie.

Approximationseigenschaften

Hervorragende Approximation des Kreises bei überschaubarer Komplexität der Formeln und Konstruktionen.

Fazit

Das regelmäßige Zehneck verbindet mathematische Schönheit mit praktischer Anwendbarkeit. Seine Verbindung zum goldenen Schnitt, die Konstruierbarkeit mit klassischen Mitteln und die vielfältigen Anwendungsmöglichkeiten machen es zu einem zeitlos interessanten geometrischen Objekt. Von der reinen Mathematik bis hin zu Design und Technik zeigt es die Eleganz und Universalität geometrischer Prinzipien.

Ist diese Seite hilfreich?            
Vielen Dank für Ihr Feedback!

Das tut uns leid

Wie können wir die Seite verbessern?

Weitere Polygone

Dreieck • Viereck (Quadrat) • Fünfeck (Pentagon) • Sechseck (Hexagon) • Siebeneck (Heptagon) • Achteck (Oktagon) • Neuneck (Nonagon) • Zehneck (Dekagon) • Elfeck (Hendekagon) • Zwölfeck (Dodekagon) • Sechzehneck (Hexadekagon) • Regelmäßiges N-Eck • Regelmäßigen Vieleckring • Konkaves gleichseitigen Sechseck • Achsensymmetrisches Fünfeck • Verlängertes Sechseck • Verlängertes Achteck • Pentagramm • Hexagramm • Oktagramm • Sterns von Lakshmi