Elfeck (Hendekagon) berechnen
Rechner und Formeln für regelmäßige Elfecke
Hendekagon Rechner
Regelmäßiges Elfeck
Ein regelmäßiges Hendekagon hat 11 gleich lange Seiten und 11 gleich große Winkel (≈147,3°). Die Zahl 11 ist eine Primzahl.
Regelmäßiges Hendekagon
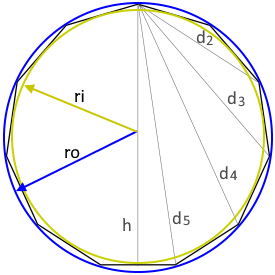
Das Diagramm zeigt ein regelmäßiges Elfeck mit allen relevanten Parametern.
Alle 11 Seiten sind gleich lang, alle Innenwinkel betragen ≈147,3°.
|
|
Eigenschaften eines regelmäßigen Elfecks
Ein regelmäßiges Elfeck (Hendekagon) ist ein besonderes geometrisches Objekt:
- 11 gleiche Seiten: Alle Seitenlängen sind identisch
- 11 gleiche Winkel: Jeder Innenwinkel beträgt ≈147,273°
- Winkelsumme: 9 × 180° = 1620°
- Primzahl 11: Besondere mathematische Eigenschaften
- Zentrumswinkel: 360°/11 ≈ 32,727° pro Segment
- Konstruktion: Komplexe geometrische Konstruktion
Das Elfeck und die Primzahl 11
Das regelmäßige Elfeck ist ein Primzahl-Polygon mit besonderen Eigenschaften:
Primzahl-Eigenschaften
- 11 ist unteilbar (nur durch 1 und 11)
- Keine einfachen Symmetrie-Unterteilungen
- Zentrumswinkel ist irrational (360°/11)
- Trigonometrische Werte sind algebraisch
Mathematische Herausforderung
- Komplexe Konstruktion mit Zirkel und Lineal
- Näherungsverfahren oft notwendig
- Verbindung zur Zahlentheorie
- Cyclotomische Polynome 11. Grades
Konstruktion und mathematische Besonderheiten
Das regelmäßige Elfeck stellt besondere konstruktive Herausforderungen:
Konstruktionsmethoden
- Mit Zirkel und Lineal konstruierbar (Gauß)
- Erfordert Lösung eines Polynoms 10. Grades
- Näherungskonstruktionen sind praktikabler
- Zentrumswinkel: 360°/11 ≈ 32,727°
Trigonometrische Werte
- cos(π/11) und sin(π/11) sind algebraisch
- Exakte Werte sehr komplex
- Numerische Approximation üblich
- Verbindung zu Gaußschen Perioden
Anwendungen des regelmäßigen Elfecks
Regelmäßige Elfecke finden spezielle Anwendungen:
Numismatik & Medaillen
- Sondermünzen mit Elfeck-Form (selten)
- Sammlermedaillen und Auszeichnungen
- Historische Jetons und Token
- Künstlerische Prägungen
Kunst & Design
- Moderne Kunstobjekte und Skulpturen
- Grafische Muster und Ornamente
- Architektonische Detailelemente
- Symmetrische Designstudien
Wissenschaft & Mathematik
- Zahlentheorie und Primzahl-Forschung
- Konstruktive Geometrie-Studien
- Symmetriegruppen-Untersuchungen
- Algorithmische Geometrie
Technik & Engineering
- Spezielle Zahnrad-Konfigurationen
- Rotations-symmetrische Bauteile
- Sensor-Arrays mit 11-facher Symmetrie
- Optische Systeme und Blenden
Formeln für das regelmäßige Elfeck (Hendekagon)
Flächeninhalt A
Mit tan(π/11) ≈ 0.2936
Umfang P
Einfach: 11-mal die Seitenlänge
Diagonale d₂
Kürzeste Diagonale
Diagonale d₃
Mittlere kurze Diagonale
Diagonale d₄
Mittlere lange Diagonale
Diagonale d₅ (längste)
Längste Diagonale
Höhe h
Mit tan(π/22) ≈ 0.1409
Innenkreisradius rᵢ
Apothem des Elfecks
Umkreisradius rₐ
Mit sin(π/11) ≈ 0.2817
Rechenbeispiel für ein Hendekagon
Gegeben
Gesucht: Alle Eigenschaften des regelmäßigen Elfecks
1. Grundmaße berechnen
Umfang und Flächeninhalt
2. Radien berechnen
Umkreis- und Innenkreisradius
3. Alle Diagonalen
Alle vier verschiedenen Diagonallängen
4. Vollständige Zusammenfassung
Komplette Charakterisierung des regelmäßigen Elfecks
Das regelmäßige Elfeck in Mathematik und Theorie
Das regelmäßige Elfeck nimmt eine besondere Stellung unter den Polygonen ein, da es zur Klasse der Primzahl-Polygone gehört. Diese Eigenschaft verleiht ihm einzigartige mathematische Charakteristika und macht es zu einem interessanten Studienobjekt in der konstruktiven Geometrie und Zahlentheorie.
Primzahl-Eigenschaften und mathematische Bedeutung
Die mathematischen Eigenschaften des regelmäßigen Elfecks werden durch die Primzahl 11 geprägt:
- Unteilbarkeit: 11 ist nur durch 1 und sich selbst teilbar
- Irrationale Winkel: 360°/11 ≈ 32,727° ist ein irrationaler Bruch von π
- Komplexe Konstruktion: Erfordert Lösung eines Polynoms 10. Grades
- Gaußsche Theorie: Konstruierbar nach dem Gauß-Wantzel-Theorem
- Cyclotomische Polynome: Verbindung zur höheren Algebra
Konstruktive Geometrie und Näherungsverfahren
Die Konstruktion des regelmäßigen Elfecks stellt besondere Herausforderungen dar:
Exakte Konstruktion
Nach Gauß ist das regelmäßige Elfeck mit Zirkel und Lineal konstruierbar, jedoch erfordert dies die Lösung sehr komplexer algebraischer Gleichungen.
Praktische Näherungen
In der Praxis werden oft Näherungsverfahren verwendet, die suffizient genaue Ergebnisse für technische Anwendungen liefern.
Trigonometrische Werte
Die Werte von cos(π/11) und sin(π/11) sind zwar algebraisch, aber ihre exakte Form ist äußerst komplex und unhandlich.
Numerische Methoden
Moderne Berechnungen verwenden numerische Approximationen, die für alle praktischen Zwecke ausreichend präzise sind.
Anwendungen und wissenschaftliche Relevanz
Trotz seiner konstruktiven Komplexität findet das Elfeck interessante Anwendungen:
- Zahlentheorie-Forschung: Studium von Primzahl-Eigenschaften und cyclotomischen Feldern
- Computergrafik: Algorithmen für regelmäßige Polygone mit Primzahl-Seitenzahl
- Kristallographie: Theoretische Strukturen mit 11-facher Symmetrie (Quasikristalle)
- Optik: Spezielle Blenden und Apertur-Designs mit ungerader Symmetrie
- Maschinenbau: Zahnräder und rotierende Systeme mit Primzahl-Teilung
Moderne computationale Aspekte
In der digitalen Ära gewinnt das Elfeck neue Bedeutung:
Algorithmic Geometry
Effiziente Algorithmen zur Berechnung und Darstellung von Primzahl-Polygonen in CAD-Systemen und Computergrafik.
Numerical Analysis
Entwicklung präziser numerischer Methoden zur Approximation der trigonometrischen Funktionen von π/11.
Symmetry Studies
Untersuchung von Symmetriegruppen und deren Anwendungen in der theoretischen Physik und Materialwissenschaft.
Computational Number Theory
Verwendung in Algorithmen zur Primzahlforschung und algebraischen Strukturanalyse.
Zusammenfassung
Das regelmäßige Elfeck steht als Beispiel für die Verbindung zwischen reiner Mathematik und praktischer Anwendung. Seine Primzahl-Eigenschaften machen es zu einem faszinierenden Studienobjekt für Zahlentheorie und konstruktive Geometrie, während moderne numerische Methoden seine praktische Anwendbarkeit in Technik und Wissenschaft ermöglichen. Es zeigt, wie auch scheinbar "unpraktische" mathematische Objekte in der digitalen Welt neue Relevanz erlangen können.
|
|
|
|