Bessel-I Funktion berechnen
Online Rechner zur modifizierten Bessel-Funktion Iᵥ(z) der ersten Art - Exponentielles Verhalten für Wärmeleitung und Wellenleitern
Bessel-I Funktion Rechner
Modifizierte Bessel-Funktion
Die Iᵥ(z) oder modifizierte Bessel-Funktion zeigt exponentielles Verhalten statt Oszillation und ist wichtig für Zylindersymmetrie.
Bessel-I Funktionskurve
Mauszeiger auf der Grafik zeigt die Werte an.
Die modifizierte Bessel-Funktion zeigt exponentielles Wachstum.
|
|
Warum exponentielles statt oszillierendes Verhalten?
Die modifizierte Bessel-Funktion unterscheidet sich fundamental von der gewöhnlichen Bessel-Funktion:
- Exponentielles Wachstum: Iᵥ(z) wächst exponentiell für große z
- Keine Oszillation: Kein periodisches Auf und Ab
- Physikalische Relevanz: Beschreibt Diffusion und Wärmeleitung
- Zylindersymmetrie: Wichtig für zylindrische Koordinaten
- Monotonie: Streng monoton wachsend für z > 0
- Asymptotik: Iᵥ(z) ~ e^z/√(2πz) für große z
Anwendungen in zylindrischen Systemen
Die modifizierte Bessel-Funktion ist fundamental für Probleme mit Zylindersymmetrie:
Wärmeleitung
- Temperaturverteilung in Zylindern
- Wärmeleitung in Rohrleitungen
- Kühlung/Erwärmung zylindrischer Objekte
Elektromagnetik
- Wellenleiter (Koaxialkabel)
- Elektromagnetische Felder
- Antennentheorie
Formeln zur Bessel-I Funktion
Definition über J-Funktion
Beziehung zur gewöhnlichen Bessel-Funktion
Rekursionsformel
Beziehung zwischen Ordnungen
Reihenentwicklung
Potenzreihenentwicklung
Integraldarstellung
Für ganzzahlige Ordnung n
Asymptotische Form
Für große z
Spezielle Werte
Wichtige Werte
Symmetrieeigenschaften
Für ganzzahlige n
Verhalten bei z = 0
Grenzverhalten im Ursprung
Anwendungsgebiete
Wärmeleitung, elektromagnetische Wellenleiter, Diffusionsprozesse, statistische Mechanik.
Wronskische Determinante
Mit K-Funktion (zweiter Art)
Vergleich der Bessel-Funktionen
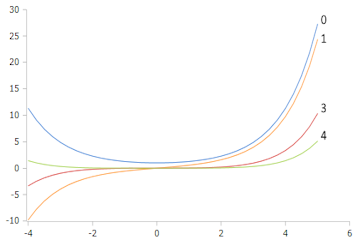
Bessel-I Funktionen (Ordnung 0,1,3,4)
Alle zeigen exponentielles Wachstum für große z-Werte. Höhere Ordnungen starten flacher, wachsen aber ebenfalls exponentiell.
Charakteristische Eigenschaften
- I₀(z) startet bei 1 und wächst monoton
- Iₙ(z) mit n > 0 startet bei 0
- Alle Funktionen sind streng konvex
- Asymptotisch: ~ e^z/√(2πz)
Ausführliche Beschreibung der Bessel-I Funktion
Mathematische Definition
Die modifizierte Bessel-Funktion der ersten Art Iᵥ(z) ist eine fundamentale Lösung der modifizierten Bessel-Differentialgleichung. Im Gegensatz zur gewöhnlichen Bessel-Funktion zeigt sie exponentielles Wachstum statt oszillierendes Verhalten.
Verwendung des Rechners
Geben Sie die Ordnungszahl ν (ganze Zahl) und das Argument z (positive reelle Zahl) ein. Bei negativem z kann das Ergebnis komplex werden.
Historischer Hintergrund
Die modifizierten Bessel-Funktionen wurden von Friedrich Bessel (1784-1846) entwickelt und später von Lord Kelvin und anderen für physikalische Anwendungen systematisiert. Der Name "modifiziert" bezieht sich auf die Transformation iz → z.
Eigenschaften und Anwendungen
Physikalische Anwendungen
- Wärmeleitung in zylindrischen Objekten
- Elektromagnetische Wellenleiter
- Diffusionsprozesse mit Zylindersymmetrie
- Membranschwingungen
Mathematische Eigenschaften
- Exponentielles Wachstum für große z
- Strenge Monotonie für z > 0
- Symmetrie: I₋ₙ(z) = Iₙ(z) für ganzzahlige n
- Konvexität für alle reellen z > 0
Numerische Aspekte
- Stabilität: Numerisch stabil für z ≥ 0
- Skalierung: Exponentielles Wachstum erfordert Vorsicht
- Rekursion: Effiziente Berechnung über Rekursionsformeln
- Asymptotik: Asymptotische Entwicklungen für große z
Interessante Fakten
- Die Funktion I₀(z) beschreibt die Wahrscheinlichkeitsdichte der von Mises-Verteilung
- Für sehr kleine z: Iᵥ(z) ≈ (z/2)^ν / Γ(ν+1)
- Die Funktionen erfüllen die modifizierte Bessel-Differentialgleichung
- Wichtig in der Quantenfeldtheorie und statistischen Mechanik
Berechnungsbeispiele
Beispiel 1
I₀(1) ≈ 1.266
Bessel-I nullter Ordnung bei z = 1
Beispiel 2
I₁(2) ≈ 1.591
Bessel-I erster Ordnung bei z = 2
Beispiel 3
I₂(3) ≈ 2.245
Bessel-I zweiter Ordnung bei z = 3
Bessel-Funktionen Klassifikation
Bessel erster Gattung (Jᵥ)
Lösungen der Standard-Bessel-Gleichung:
Oszillierendes Verhalten, endlich bei z = 0 für ν ≥ 0.
Bessel zweiter Gattung (Yᵥ)
Auch Neumann-Funktionen genannt:
Singulär bei z = 0, oszillierend für große z.
Modifizierte Bessel (Iᵥ, Kᵥ)
Exponentielles Verhalten:
Iᵥ: exponentiell wachsend, Kᵥ: exponentiell abfallend.
Differentialgleichung und Lösungstheorie
Modifizierte Bessel-Gleichung
Die modifizierte Bessel-Gleichung mit Parameter ν.
Allgemeine Lösung
Linearkombination der beiden linear unabhängigen Lösungen.
|
|
|
|