Modified Bessel-I Function for Complex Numbers

Calculation of the modified Bessel function \(I_\nu(z)\) of the first kind for complex arguments

Bessel-I Function Calculator

Modified Bessel Function \(I_\nu(z)\)

The modified Bessel function \(I_\nu(z)\) of the first kind exhibits exponential rather than oscillatory behavior and is a solution to the modified Bessel differential equation.

Complex Argument z = a + bi
+
i
Integer or rational order of the Bessel function
Calculation Result
\(I_\nu(z)\) =

Bessel-I Properties

Behavior

Exponential

Grows with |z|

Non-oscillating
Kind

First Kind

Type: \(I_\nu\)

Regular at origin
Order

ν ∈ ℝ

Any real number

Integer or rational
Argument

z ∈ ℂ

Complex: a+bi

Real and imaginary part
Important Properties
  • Solution of the modified Bessel DDE
  • Exponential growth for large |z|
  • Symmetry relation: \(I_{-n}(z) = I_n(z)\) for integer n
  • Limit: \(\lim_{z \to 0} I_\nu(z) = 0\) for ν > 0
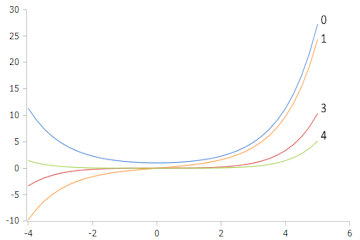
BesselI

Plot of the Bessel-I function with orders 0, 1, 3, and 4

Mathematical Definition of the Modified Bessel Function

The modified Bessel function of the first kind \(I_\nu(z)\) is defined by:

Power Series Expansion
\[I_\nu(z) = \sum_{m=0}^{\infty} \frac{1}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Where \(\Gamma\) is the gamma function

Relationship to Bessel-J Function
\[I_\nu(z) = i^{-\nu} J_\nu(iz)\]

Transformation of the ordinary Bessel function

Modified Bessel DDE
\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} - (z^2 + \nu^2)w = 0\]

Differential equation with solution \(w = I_\nu(z)\)

Important Formulas and Properties

Symmetry Relations
\[I_{-n}(z) = I_n(z) \quad \text{(for integer n)}\] \[I_\nu(-z) = (-1)^\nu I_\nu(z) \quad \text{(for integer ν)}\]

Important symmetry properties of the function

Asymptotic Behavior
\[I_\nu(z) \sim \frac{e^{|z|}}{\sqrt{2\pi|z|}} \quad \text{for } |z| \to \infty\]

Exponential growth for large arguments

Special Values
\[I_0(0) = 1\] \[I_\nu(0) = 0 \quad \text{for } \nu > 0\]

Values at the origin

Recurrence Relations
\[I_{\nu-1}(z) - I_{\nu+1}(z) = \frac{2\nu}{z} I_\nu(z)\] \[I_{\nu-1}(z) + I_{\nu+1}(z) = 2 I_\nu'(z)\]

Relationships between different orders

Applications and Practical Examples

Heat Conduction
Cylindrical symmetry Time-dependent Diffusion equation Temperature distribution
Electromagnetism
Waveguides:
Cylindrically symmetric modes
TM and TE modes
Antenna Engineering:
Radiation characteristics
Far-field approximation
Quantum Mechanics

Hydrogen atom

Coulomb potential

Radial wave functions

Mechanics & Acoustics

Membrane vibrations

Drumhead modes

Sound propagation

Resonance frequencies

Bessel Functions - Detailed Mathematical Description

Historical Context

Bessel functions were originally defined by the mathematician Daniel Bernoulli in connection with vibrations of a hanging chain and later generalized and systematically studied by Friedrich Wilhelm Bessel.

Classification of Bessel Functions:
• Ordinary Bessel Functions: \(J_\nu(z)\), \(Y_\nu(z)\)
• Modified Bessel Functions: \(I_\nu(z)\), \(K_\nu(z)\)
• Hankel Functions: \(H_\nu^{(1)}(z)\), \(H_\nu^{(2)}(z)\)

Modified vs. Ordinary Bessel Functions

While the ordinary Bessel functions \(J_\nu(x)\) oscillate for real arguments, the modified Bessel functions \(I_\nu(x)\) exhibit exponential behavior. This property makes them particularly suitable for describing diffusion processes and exponentially growing or decaying phenomena.

Important Differences

Ordinary Bessel Function \(J_\nu(x)\): Oscillates and decays like \(\sqrt{\frac{2}{\pi x}} \cos(x - \frac{\nu\pi}{2} - \frac{\pi}{4})\)
Modified Bessel Function \(I_\nu(x)\): Grows exponentially like \(\frac{e^x}{\sqrt{2\pi x}}\)

Complex Arguments

For complex arguments z = x + iy, the Bessel functions extend to analytic functions of the complex plane. The modified Bessel function \(I_\nu(z)\) retains its characteristic properties.

Complex Properties:
• Analytic continuation to all of ℂ
• Branch points at z = 0
• Asymptotic behavior for |z| → ∞

Differential Equation

The modified Bessel function \(I_\nu(z)\) is a solution of the modified Bessel differential equation:

\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} - (z^2 + \nu^2)w = 0\]

This equation differs from the ordinary Bessel DDE by the sign of the \(z^2\) term.

Numerical Calculation

Various methods are used for practical calculation:

  • Power series: For small |z|
  • Asymptotic expansion: For large |z|
  • Recurrence relations: Between different orders
  • Integral representations: For special applications

Extended Mathematical Properties

Integral Representations
\[I_\nu(z) = \frac{1}{\pi} \int_0^\pi e^{z\cos\theta} \cos(\nu\theta) d\theta\]

For Re(z) > 0

Generating Function
\[e^{\frac{z}{2}(t + \frac{1}{t})} = \sum_{n=-\infty}^{\infty} I_n(z) t^n\]

Laurent expansion

Addition Theorems
\[I_\nu(z_1 + z_2) = \sum_{k=-\infty}^{\infty} I_k(z_1) I_{\nu-k}(z_2)\]

Under certain conditions

Practical Calculation Tips
  • Small arguments: Use power series
  • Large arguments: Asymptotic formulas
  • Integer order: Utilize recurrence relations
  • Complex arguments: Beware of branch cuts
  • Numerical stability: Consider scaling
  • Precision: Sufficient terms in series expansion

Bessel Functions - Complete Definitions

Bessel Functions of the First Kind (\(J_\nu\))

The Bessel function of the first kind of order n is defined as:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Here \(\Gamma\) is the gamma function. At the origin (\(z = 0\)) these functions are finite for integer values of \(\nu\). For integer values of \(\nu\), the relationship holds:

\[J_{-\nu}(z) = (-1)^{\nu} J_{\nu}(z)\]

Bessel Functions of the Second Kind (\(Y_\nu\))

The Bessel function of the second kind of order n is defined as:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \ pi)}\]

Modified Bessel Functions (\(I_\nu, K_\nu\))

The modified Bessel function of the first kind of order n is defined as:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

The modified Bessel function of the second kind of order n is defined as:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Important Properties

These functions play an important role in describing vibrations of a circular membrane, electromagnetic waves in cylindrical waveguides, heat conduction in cylindrical objects, acoustic membranes, and much more. They are an indispensable tool for many problems of wave propagation and static potentials in physics and engineering.


More complex functions

Absolute value (abs) • Angle • Conjugate • Division • Exponent • Logarithm to base 10 • Multiplication • Natural logarithm • Polarform • Power • Root • Reciprocal • Square root •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy function • Derivative Airy function •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye •