Modifizierte Bessel-I Funktion für komplexe Zahlen

Berechnung der modifizierten Bessel-Funktion \(I_\nu(z)\) der ersten Art für komplexe Argumente

Bessel-I Funktionsrechner

Modifizierte Bessel-Funktion \(I_\nu(z)\)

Die modifizierte Bessel-Funktion \(I_\nu(z)\) der ersten Art zeigt exponentielles statt oszillierendes Verhalten und ist eine Lösung der modifizierten Bessel-Differentialgleichung.

Komplexes Argument z = a + bi
+
i
Ganzzahlige oder rationale Ordnung der Bessel-Funktion
Berechnungsergebnis
\(I_\nu(z)\) =

Bessel-I Eigenschaften

Verhalten

Exponentiell

Wächst mit |z|

Nicht oszillierend
Art

Erste Art

Typ: \(I_\nu\)

Am Ursprung regulär
Ordnung

ν ∈ ℝ

Beliebige reelle Zahl

Ganzzahlig oder rational
Argument

z ∈ ℂ

Komplex: a+bi

Reell- und Imaginärteil
Wichtige Eigenschaften
  • Lösung der modifizierten Bessel-DGL
  • Exponentielles Wachstum für große |z|
  • Symmetrierelation: \(I_{-n}(z) = I_n(z)\) für ganzzahlige n
  • Grenzwert: \(\lim_{z \to 0} I_\nu(z) = 0\) für ν > 0
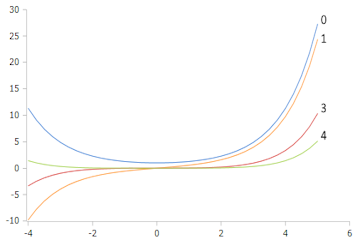
BesselI

Plot der Bessel-I Funktion mit den Ordnungszahlen 0, 1, 3 und 4

Mathematische Definition der modifizierten Bessel-Funktion

Die modifizierte Bessel-Funktion erster Art \(I_\nu(z)\) ist definiert durch:

Potenzreihenentwicklung
\[I_\nu(z) = \sum_{m=0}^{\infty} \frac{1}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Wobei \(\Gamma\) die Gammafunktion ist

Beziehung zur Bessel-J Funktion
\[I_\nu(z) = i^{-\nu} J_\nu(iz)\]

Transformation der gewöhnlichen Bessel-Funktion

Modifizierte Bessel-DGL
\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} - (z^2 + \nu^2)w = 0\]

Differentialgleichung mit Lösung \(w = I_\nu(z)\)

Wichtige Formeln und Eigenschaften

Symmetrierelationen
\[I_{-n}(z) = I_n(z) \quad \text{(für ganzzahlige n)}\] \[I_\nu(-z) = (-1)^\nu I_\nu(z) \quad \text{(für ganzzahlige ν)}\]

Wichtige Symmetrieeigenschaften der Funktion

Asymptotisches Verhalten
\[I_\nu(z) \sim \frac{e^{|z|}}{\sqrt{2\pi|z|}} \quad \text{für } |z| \to \infty\]

Exponentielles Wachstum für große Argumente

Spezielle Werte
\[I_0(0) = 1\] \[I_\nu(0) = 0 \quad \text{für } \nu > 0\]

Werte am Ursprung

Rekurrenzrelationen
\[I_{\nu-1}(z) - I_{\nu+1}(z) = \frac{2\nu}{z} I_\nu(z)\] \[I_{\nu-1}(z) + I_{\nu+1}(z) = 2 I_\nu'(z)\]

Beziehungen zwischen verschiedenen Ordnungen

Anwendungen und praktische Beispiele

Wärmeleitung
Zylindersymmetrie Zeitabhängig Diffusionsgleichung Temperaturverteilung
Elektromagnetismus
Wellenleiter:
Zylindersymmetrische Modi
TM und TE Moden
Antennentechnik:
Strahlungscharakteristik
Fernfeldapproximation
Quantenmechanik

Wasserstoffatom

Coulomb-Potential

Radiale Wellenfunktionen

Mechanik & Akustik

Membranschwingungen

Trommelfell-Modi

Schallausbreitung

Resonanzfrequenzen

Bessel-Funktionen - Detaillierte mathematische Beschreibung

Historischer Kontext

Die Bessel-Funktionen wurden ursprünglich von dem Mathematiker Daniel Bernoulli im Zusammenhang mit Schwingungen einer hängenden Kette definiert und später von Friedrich Wilhelm Bessel verallgemeinert und systematisch untersucht.

Klassifikation der Bessel-Funktionen:
• Gewöhnliche Bessel-Funktionen: \(J_\nu(z)\), \(Y_\nu(z)\)
• Modifizierte Bessel-Funktionen: \(I_\nu(z)\), \(K_\nu(z)\)
• Hankel-Funktionen: \(H_\nu^{(1)}(z)\), \(H_\nu^{(2)}(z)\)

Modifizierte vs. Gewöhnliche Bessel-Funktionen

Während die gewöhnlichen Bessel-Funktionen \(J_\nu(x)\) für reelle Argumente oszillieren, zeigen die modifizierten Bessel-Funktionen \(I_\nu(x)\) ein exponentielles Verhalten. Diese Eigenschaft macht sie besonders geeignet für die Beschreibung von Diffusionsprozessen und exponentiell wachsenden oder abklingenden Phänomenen.

Wichtige Unterschiede

Gewöhnliche Bessel-Funktion \(J_\nu(x)\): Oszilliert und klingt ab wie \(\sqrt{\frac{2}{\pi x}} \cos(x - \frac{\nu\pi}{2} - \frac{\pi}{4})\)
Modifizierte Bessel-Funktion \(I_\nu(x)\): Wächst exponentiell wie \(\frac{e^x}{\sqrt{2\pi x}}\)

Komplexe Argumente

Für komplexe Argumente z = x + iy erweitern sich die Bessel-Funktionen zu analytischen Funktionen der komplexen Ebene. Die modifizierte Bessel-Funktion \(I_\nu(z)\) behält dabei ihre charakteristischen Eigenschaften bei.

Komplexe Eigenschaften:
• Analytische Fortsetzung auf ganz ℂ
• Verzweigungspunkte bei z = 0
• Asymptotisches Verhalten für |z| → ∞

Differentialgleichung

Die modifizierte Bessel-Funktion \(I_\nu(z)\) ist eine Lösung der modifizierten Bessel-Differentialgleichung:

\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} - (z^2 + \nu^2)w = 0\]

Diese Gleichung unterscheidet sich von der gewöhnlichen Bessel-DGL durch das Vorzeichen des \(z^2\)-Terms.

Numerische Berechnung

Für die praktische Berechnung werden verschiedene Methoden verwendet:

  • Potenzreihe: Für kleine |z|
  • Asymptotische Entwicklung: Für große |z|
  • Rekurrenzrelationen: Zwischen verschiedenen Ordnungen
  • Integraldarstellungen: Für spezielle Anwendungen

Erweiterte mathematische Eigenschaften

Integraldarstellungen
\[I_\nu(z) = \frac{1}{\pi} \int_0^\pi e^{z\cos\theta} \cos(\nu\theta) d\theta\]

Für Realteil(z) > 0

Erzeugende Funktion
\[e^{\frac{z}{2}(t + \frac{1}{t})} = \sum_{n=-\infty}^{\infty} I_n(z) t^n\]

Laurent-Entwicklung

Additionstheoreme
\[I_\nu(z_1 + z_2) = \sum_{k=-\infty}^{\infty} I_k(z_1) I_{\nu-k}(z_2)\]

Unter bestimmten Bedingungen

Praktische Berechnungstipps
  • Kleine Argumente: Potenzreihe verwenden
  • Große Argumente: Asymptotische Formeln
  • Ganzzahlige Ordnung: Rekurrenzrelationen nutzen
  • Komplexe Argumente: Vorsicht bei Verzweigungsschnitten
  • Numerische Stabilität: Skalierung beachten
  • Präzision: Genügend Terme in Reihenentwicklung

Bessel-Funktionen - Vollständige Definitionen

Bessel-Funktionen erster Gattung (\(J_\nu\))

Die Bessel-Funktion erster Gattung n-ter Ordnung ist definiert als:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Hierbei ist \(\Gamma\) die Gammafunktion. Im Ursprung (\(z = 0\)) sind diese Funktionen für ganzzahlige Werte von \(\nu\) endlich. Für ganzzahlige Werte von \(\nu\) gilt die Beziehung:

\[J_{-\nu}(z) = (-1)^{\nu} J_{\nu}(z)\]

Bessel-Funktionen zweiter Gattung (\(Y_\nu\))

Die Bessel-Funktion zweiter Gattung n-ter Ordnung ist definiert als:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Modifizierte Bessel-Funktionen (\(I_\nu, K_\nu\))

Die modifizierte Bessel-Funktion erster Art n-ter Ordnung ist definiert als:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

Die modifizierte Bessel-Funktion zweiter Art n-ter Ordnung ist definiert als:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Wichtige Eigenschaften

Diese Funktionen spielen eine wichtige Rolle bei der Beschreibung von Schwingungen einer kreisförmigen Membran, elektromagnetischen Wellen in zylindrischen Wellenleitern, Wärmeleitung in zylindrischen Objekten, akustischen Membranen und vielem mehr. Sie sind ein unverzichtbares Werkzeug für viele Probleme der Wellenausbreitung und statischer Potentiale in der Physik und Ingenieurwissenschaften.


Weitere Komplexe Funktionen

Betrag / Absolutwert • Division • Exponent • Konjugierte • Logarithmus zur Basis 10 • Multiplikation • Natürlicher Logarithmus • Polarform • Quadratwurzel • Wurzel • Potenz • Reziprok • Winkel •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy Funktion • Abgeleitete Airy Funktion •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye