Exponentially Scaled Bessel-Ye Function for Complex Numbers

Calculation of the exponentially scaled Bessel function \(Y_e(z) = e^{-|z|} Y_\nu(z)\) of the second kind

Bessel-Ye Function Calculator

Exponentially Scaled Bessel Function \(Y_e(z)\)

The exponentially scaled Bessel function of the second kind \(Y_e(z) = e^{-|z|} Y_\nu(z)\) prevents numerical overflows for large arguments and combines oscillatory behavior with numerical stability.

Complex Argument z = a + bi
+
i
Integer or rational order of the Bessel function
Calculation Result
\(Y_e(z)\) =

Bessel-Ye Properties

Scaling

Exponential

Factor: \(e^{-|z|}\)

Prevents overflow
Behavior

Oscillatory

Type: \(Y_\nu(z)\)

Damped oscillation
Order

ν ∈ ℝ

Any real number

Integer or rational
Argument

z ∈ ℂ

Complex: a+bi

Real and imaginary part
Important Properties
  • Numerically stable calculation for large |z|
  • Combines oscillation with exponential damping
  • Defined as: \(Y_e(z) = e^{-|z|} Y_\nu(z)\)
  • Asymptotically: \(Y_e(z) \sim \frac{1}{\sqrt{2\pi|z|}}\) for |z| → ∞
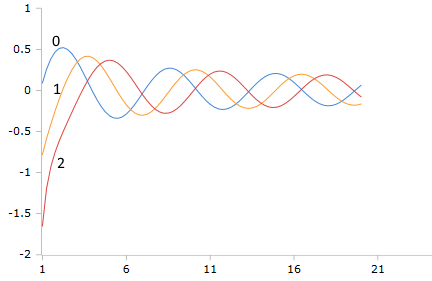
BesselY

Plot of the Bessel-Y function (before exponential scaling)

Definition of the Exponentially Scaled Bessel-Ye Function

The exponentially scaled Bessel function of the second kind \(Y_e(z)\) is defined as:

Scaled Definition
\[Y_e(z) = e^{-|z|} Y_\nu(z) = e^{-|z|} \cdot \frac{J_\nu(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Exponentially scaled version to avoid numerical overflows in oscillating functions

Numerical Stability
\[|Y_e(z)| \leq \frac{C}{\sqrt{|z|}}\]

Bounded for large |z|, prevents oscillation overflow

Relationship to Bessel-Y
\[Y_\nu(z) = e^{|z|} Y_e(z)\]

Back-transformation to the original function

Important Properties of the Scaled Bessel-Ye Function

Asymptotic Behavior
\[Y_e(z) \sim \frac{1}{\sqrt{2\pi|z|}} \sin\left(|z| - \frac{\nu\pi}{2} - \frac{\pi}{4}\right) e^{-|z|}\]

Oscillation with exponential damping for large |z|

Numerical Advantages
\[\max|Y_e(z)| < \infty \quad \text{for all } z\]

Bounded values prevent overflow despite oscillation

Scaling Factor
\[s(z) = e^{-|z|} = e^{-\sqrt{\text{Re}(z)^2 + \text{Im}(z)^2}}\]

Exponential damping factor based on the modulus of z

Recurrence Relations
\[Y_{e,\nu-1}(z) + Y_{e,\nu+1}(z) = \frac{2\nu}{z} Y_{e,\nu}(z)\]

Scaled recurrence relations apply analogously

Applications of the Scaled Bessel-Ye Function

Numerical Analysis
Large arguments Oscillation control Stable algorithms Precise calculation
Wave Physics
Far-field:
Exterior waves
Scattering problems
Acoustics:
Radiation patterns
Resonance analysis
Electromagnetism

Waveguides

Antenna theory

Far-field patterns

Mathematical Physics

Boundary value problems

Green's functions

Exterior solutions

Hankel functions

Exponentially Scaled Bessel-Ye Functions - Detailed Description

Numerical Stability with Oscillation and Singularity

The exponentially scaled Bessel-Ye function \(Y_e(z)\) was developed to solve the numerical problems of the Bessel function \(Y_\nu(z)\) for large arguments, where the oscillations can become very large, while the function simultaneously has a singularity at the origin.

Problem Statement:
• \(Y_\nu(z)\) oscillates with increasing amplitude for large |z|
• Additionally singular at the origin
• Numerical instabilities in oscillating regions
• Difficult calculation for large arguments

Solution Approach

By the definition \(Y_e(z) = e^{-|z|} Y_\nu(z)\), the oscillating function is provided with exponential damping, so that the resulting function remains numerically stable, even for large arguments.

Advantages of Scaling

Without scaling: \(Y_\nu(100)\) can show very large oscillations
With scaling: \(Y_{e,\nu}(100)\) remains in the stable range

Mathematical Properties

The scaled function retains all important mathematical properties of the original oscillating Bessel-Y function, but is numerically more stable.

Preserved Properties:
• Recurrence relations remain valid
• Oscillatory character preserved
• Linearly independent from \(J_{e,\nu}\)
• Singularity at origin remains

Implementation

In numerical practice, the scaled version is used for large arguments and the result is back-transformed if needed:

\[Y_\nu(z) = e^{|z|} \cdot Y_e(z)\]

Back-transformation only when explicitly needed

Relationship to Hankel Functions

Scaled Hankel functions:
\(H_{e,\nu}^{(1)}(z) = J_{e,\nu}(z) + iY_{e,\nu}(z)\)
\(H_{e,\nu}^{(2)}(z) = J_{e,\nu}(z) - iY_{e,\nu}(z)\)

Comparison: Scaled vs. Unscaled

Unscaled Bessel-Y Function
Definition: \(Y_\nu(z)\)
Behavior: Oscillation with varying amplitude
Origin: Singular at z=0
Problems: Large amplitudes for large |z|
Numerics: Can become unstable
Scaled Bessel-Ye Function
Definition: \(Y_e(z) = e^{-|z|} Y_\nu(z)\)
Behavior: Damped oscillation
Origin: Singular at z=0 (preserved)
Advantages: Stable amplitudes
Range: All |z| (practically unlimited)
Practical Application Guidelines
  • Small |z| ≤ 10: Both versions usable (except near z=0)
  • Medium |z| ≤ 50: Scaled version recommended
  • Large |z| > 50: Only use scaled version
  • Exterior problems: Always scaled version
  • Far-field calculations: Prefer scaling
  • Hankel functions: Combine scaled versions

Bessel Functions - Complete Definitions and Scaling

Ordinary Bessel Functions

The Bessel function of the first kind of order n is defined as:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

The exponentially scaled version is:

\[J_e(z) = e^{-|z|} J_{\nu}(z)\]

The Bessel function of the second kind (Neumann function) is:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

The exponentially scaled Neumann function is:

\[Y_e(z) = e^{-|z|} Y_{\nu}(z)\]

Modified Bessel Functions

The modified Bessel function of the first kind is:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

The modified Bessel function of the second kind is:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Application Areas

The exponentially scaled Bessel-Ye function is particularly important for exterior problems with oscillating solutions for large arguments, far-field analyses, wave propagation, and scattering problems where both singularities and oscillations with large amplitude occur.


More complex functions

Absolute value (abs) • Angle • Conjugate • Division • Exponent • Logarithm to base 10 • Multiplication • Natural logarithm • Polarform • Power • Root • Reciprocal • Square root •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy function • Derivative Airy function •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye •