Ordinary Bessel-J Function for Complex Numbers

Calculation of the Bessel function \(J_\nu(z)\) of the first kind with oscillatory behavior

Bessel-J Function Calculator

Ordinary Bessel Function \(J_\nu(z)\)

The ordinary Bessel function \(J_\nu(z)\) of the first kind exhibits oscillatory behavior and is a solution to the Bessel differential equation.

Complex Argument z = a + bi
+
i
Integer or rational order of the Bessel function
Calculation Result
\(J_\nu(z)\) =

Bessel-J Properties

Behavior

Oscillatory

Decaying oscillations

Not exponential
Kind

First Kind

Type: \(J_\nu\)

Regular at origin
Order

ν ∈ ℝ

Any real number

Integer or rational
Argument

z ∈ ℂ

Complex: a+bi

Real and imaginary part
Important Properties
  • Solution of the Bessel differential equation
  • Oscillatory, decaying behavior for large |z|
  • Symmetry relation: \(J_{-n}(z) = (-1)^n J_n(z)\) for integer n
  • Limit: \(J_0(0) = 1\), \(J_\nu(0) = 0\) for ν > 0
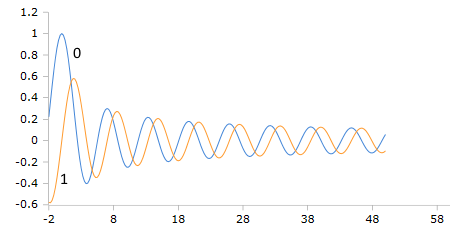
BesselJ

Plot of the Bessel-J function with orders 0 and 1

Definition of the Ordinary Bessel Function

The ordinary Bessel function of the first kind \(J_\nu(z)\) is defined by:

Power Series Expansion
\[J_\nu(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Where \(\Gamma\) is the gamma function and the factor \((-1)^m\) generates the oscillation

Bessel Differential Equation
\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} + (z^2 - \nu^2)w = 0\]

Differential equation with solution \(w = J_\nu(z)\)

Relationship to Modified Bessel-I
\[I_\nu(z) = i^{-\nu} J_\nu(iz)\]

Transformation to the modified Bessel function

Important Properties of the Bessel-J Function

Asymptotic Behavior
\[J_\nu(z) \sim \sqrt{\frac{2}{\pi z}} \cos\left(z - \frac{\nu\pi}{2} - \frac{\pi}{4}\right)\]

Oscillatory, decaying behavior for large |z|

Symmetry Relations
\[J_{-n}(z) = (-1)^n J_n(z) \quad \text{(for integer n)}\]

Important symmetry property of the ordinary Bessel function

Special Values
\[J_0(0) = 1\] \[J_\nu(0) = 0 \quad \text{for } \nu > 0\]

Values at the origin

Recurrence Relations
\[J_{\nu-1}(z) + J_{\nu+1}(z) = \frac{2\nu}{z} J_\nu(z)\] \[J_{\nu-1}(z) - J_{\nu+1}(z) = 2 J_\nu'(z)\]

Relationships between different orders

Applications of the Bessel-J Function

Wave Mechanics
Cylindrical waves Vibration modes Resonators Wave propagation
Electromagnetism
Antenna Theory:
Radiation patterns
Directivity characteristics
Waveguides:
TM and TE modes
Cutoff frequencies
Acoustics & Optics

Membrane vibrations

Slit diffraction

Interference patterns

Quantum Physics

Hydrogen atom

Cylindrically symmetric systems

Scattering problems

Eigenvalue problems

Ordinary Bessel Functions - Detailed Description

Oscillatory Behavior

The ordinary Bessel function \(J_\nu(z)\) differs fundamentally from the modified Bessel function through its oscillatory behavior.

Characteristic Properties:
• Oscillates for real arguments
• Decaying amplitude for large |z|
• Alternating signs in power series
• Finite at origin for ν ≥ 0

Historical Background

Friedrich Bessel introduced these functions in 1824 while studying planetary motion. They naturally arise in problems with cylindrical symmetry.

Physical Interpretation

\(J_0(kr)\) describes the amplitude of a cylindrical wave with wave number k at distance r from the axis. The zeros correspond to nodal lines.

Numerical Aspects

Unlike the modified Bessel functions, the ordinary Bessel functions are numerically more stable since they do not grow exponentially.

Numerical Properties:
• Bounded values for all z
• No overflow problems
• Stable recurrence relations
• Efficient calculation algorithms

Calculation Methods

Different numerical methods are used depending on the argument range:

Small |z|: Power series expansion
Medium |z|: Recurrence relations
Large |z|: Asymptotic expansions
Special values: Closed-form expressions

Special Values

Some Bessel functions have closed-form expressions, e.g.:
\(J_{1/2}(z) = \sqrt{\frac{2}{\pi z}} \sin(z)\)
\(J_{-1/2}(z) = \sqrt{\frac{2}{\pi z}} \cos(z)\)

Comparison: Bessel-J vs. Bessel-I

Ordinary Bessel-J Function
Definition: \(J_\nu(z)\) with \((-1)^m\) factor
Behavior: Oscillatory, decaying
DDE: \(z^2w'' + zw' + (z^2-\nu^2)w = 0\)
Asymptotics: \(\sim \sqrt{\frac{2}{\pi z}} \cos(...)\)
Modified Bessel-I Function
Definition: \(I_\nu(z) = i^{-\nu} J_\nu(iz)\)
Behavior: Exponentially growing
DDE: \(z^2w'' + zw' - (z^2+\nu^2)w = 0\)
Asymptotics: \(\sim \frac{e^z}{\sqrt{2\pi z}}\)
Application Guidelines
  • Wave propagation: Use Bessel-J
  • Vibration modes: Bessel-J for eigenvalues
  • Cylindrical waves: \(J_0\) and \(J_1\) most common
  • Diffusion/heat conduction: Use Bessel-I
  • Exponential growth: Modified functions
  • Large arguments: Pay attention to numerical stability

Bessel Functions - Complete Definitions and Relationships

Ordinary Bessel Functions

The Bessel function of the first kind of order n is defined as:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

The Bessel function of the second kind (Neumann function) is:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]
Applications of J-Functions

Ordinary Bessel functions are fundamental for all oscillatory phenomena with cylindrical symmetry: vibrations of drumheads, electromagnetic waves in waveguides, quantum mechanics in cylindrically symmetric potentials.

Modified Bessel Functions

The modified Bessel function of the first kind is defined as:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

The modified Bessel function of the second kind is:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Hankel Functions

Complex linear combinations:
\(H_\nu^{(1)}(z) = J_\nu(z) + iY_\nu(z)\)
\(H_\nu^{(2)}(z) = J_\nu(z) - iY_\nu(z)\)

Important for outgoing and incoming cylindrical waves.


More complex functions

Absolute value (abs) • Angle • Conjugate • Division • Exponent • Logarithm to base 10 • Multiplication • Natural logarithm • Polarform • Power • Root • Reciprocal • Square root •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy function • Derivative Airy function •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye •