Gewöhnliche Bessel-J Funktion für komplexe Zahlen

Berechnung der Bessel-Funktion \(J_\nu(z)\) der ersten Art mit oszillierendem Verhalten

Bessel-J Funktionsrechner

Gewöhnliche Bessel-Funktion \(J_\nu(z)\)

Die gewöhnliche Bessel-Funktion \(J_\nu(z)\) der ersten Art zeigt oszillierendes Verhalten und ist eine Lösung der Bessel-Differentialgleichung.

Komplexes Argument z = a + bi
+
i
Ganzzahlige oder rationale Ordnung der Bessel-Funktion
Berechnungsergebnis
\(J_\nu(z)\) =

Bessel-J Eigenschaften

Verhalten

Oszillierend

Schwingend abklingend

Nicht exponentiell
Art

Erste Art

Typ: \(J_\nu\)

Am Ursprung regulär
Ordnung

ν ∈ ℝ

Beliebige reelle Zahl

Ganzzahlig oder rational
Argument

z ∈ ℂ

Komplex: a+bi

Reell- und Imaginärteil
Wichtige Eigenschaften
  • Lösung der Bessel-Differentialgleichung
  • Oszillierendes, abklingendes Verhalten für große |z|
  • Symmetrierelation: \(J_{-n}(z) = (-1)^n J_n(z)\) für ganzzahlige n
  • Grenzwert: \(J_0(0) = 1\), \(J_\nu(0) = 0\) für ν > 0
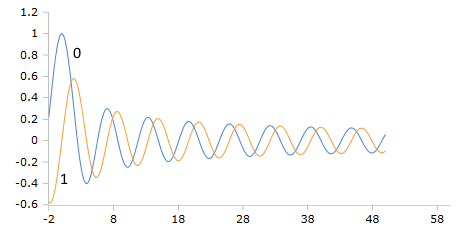
BesselJ

Plot der Bessel-J Funktion mit den Ordnungszahlen 0 und 1

Definition der gewöhnlichen Bessel-Funktion

Die gewöhnliche Bessel-Funktion erster Art \(J_\nu(z)\) ist definiert durch:

Potenzreihenentwicklung
\[J_\nu(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Wobei \(\Gamma\) die Gammafunktion ist und der Faktor \((-1)^m\) die Oszillation erzeugt

Bessel-Differentialgleichung
\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} + (z^2 - \nu^2)w = 0\]

Differentialgleichung mit Lösung \(w = J_\nu(z)\)

Beziehung zur modifizierten Bessel-I
\[I_\nu(z) = i^{-\nu} J_\nu(iz)\]

Transformation zur modifizierten Bessel-Funktion

Wichtige Eigenschaften der Bessel-J Funktion

Asymptotisches Verhalten
\[J_\nu(z) \sim \sqrt{\frac{2}{\pi z}} \cos\left(z - \frac{\nu\pi}{2} - \frac{\pi}{4}\right)\]

Oszillierendes, abklingendes Verhalten für große |z|

Symmetrierelationen
\[J_{-n}(z) = (-1)^n J_n(z) \quad \text{(für ganzzahlige n)}\]

Wichtige Symmetrieeigenschaft der gewöhnlichen Bessel-Funktion

Spezielle Werte
\[J_0(0) = 1\] \[J_\nu(0) = 0 \quad \text{für } \nu > 0\]

Werte am Ursprung

Rekurrenzrelationen
\[J_{\nu-1}(z) + J_{\nu+1}(z) = \frac{2\nu}{z} J_\nu(z)\] \[J_{\nu-1}(z) - J_{\nu+1}(z) = 2 J_\nu'(z)\]

Beziehungen zwischen verschiedenen Ordnungen

Anwendungen der Bessel-J Funktion

Wellenmechanik
Zylinderwellen Schwingungsmoden Resonatoren Wellenausbreitung
Elektromagnetismus
Antennentheorie:
Strahlungsdiagramme
Richtcharakteristiken
Wellenleiter:
TM und TE Moden
Grenzfrequenzen
Akustik & Optik

Membranschwingungen

Beugung am Spalt

Interferenzmuster

Quantenphysik

Wasserstoffatom

Zylindersymmetrische Systeme

Streuprobleme

Eigenwertprobleme

Gewöhnliche Bessel-Funktionen - Detaillierte Beschreibung

Oszillierendes Verhalten

Die gewöhnliche Bessel-Funktion \(J_\nu(z)\) unterscheidet sich fundamental von der modifizierten Bessel-Funktion durch ihr oszillierendes Verhalten.

Charakteristische Eigenschaften:
• Oszilliert für reelle Argumente
• Abklingende Amplitude für große |z|
• Alternierende Vorzeichen in Potenzreihe
• Endlich am Ursprung für ν ≥ 0

Historischer Hintergrund

Friedrich Bessel führte diese Funktionen 1824 bei der Untersuchung der Bewegung von Planeten ein. Sie treten natürlich bei Problemen mit Zylindersymmetrie auf.

Physikalische Interpretation

\(J_0(kr)\) beschreibt die Amplitude einer Zylinderwelle mit Wellenzahl k im Abstand r von der Achse. Die Nullstellen entsprechen Knotenlinien.

Numerische Aspekte

Im Gegensatz zu den modifizierten Bessel-Funktionen sind die gewöhnlichen Bessel-Funktionen numerisch stabiler, da sie nicht exponentiell wachsen.

Numerische Eigenschaften:
• Begrenzte Werte für alle z
• Keine Overflow-Probleme
• Stabile Rekurrenzrelationen
• Effiziente Berechnungsalgorithmen

Berechnungsmethoden

Verschiedene numerische Methoden werden je nach Argumentbereich verwendet:

Kleine |z|: Potenzreihenentwicklung
Mittlere |z|: Rekurrenzrelationen
Große |z|: Asymptotische Entwicklungen
Spezialwerte: Geschlossene Ausdrücke

Spezielle Werte

Einige Bessel-Funktionen haben geschlossene Ausdrücke, z.B.:
\(J_{1/2}(z) = \sqrt{\frac{2}{\pi z}} \sin(z)\)
\(J_{-1/2}(z) = \sqrt{\frac{2}{\pi z}} \cos(z)\)

Vergleich: Bessel-J vs. Bessel-I

Gewöhnliche Bessel-J Funktion
Definition: \(J_\nu(z)\) mit \((-1)^m\) Faktor
Verhalten: Oszillierend, abklingend
DGL: \(z^2w'' + zw' + (z^2-\nu^2)w = 0\)
Asymptotik: \(\sim \sqrt{\frac{2}{\pi z}} \cos(...)\)
Modifizierte Bessel-I Funktion
Definition: \(I_\nu(z) = i^{-\nu} J_\nu(iz)\)
Verhalten: Exponentiell wachsend
DGL: \(z^2w'' + zw' - (z^2+\nu^2)w = 0\)
Asymptotik: \(\sim \frac{e^z}{\sqrt{2\pi z}}\)
Anwendungsrichtlinien
  • Wellenpropagation: Bessel-J verwenden
  • Schwingungsmode: Bessel-J für Eigenwerte
  • Zylinderwellen: \(J_0\) und \(J_1\) am häufigsten
  • Diffusion/Wärmeleitung: Bessel-I verwenden
  • Exponentielles Wachstum: Modifizierte Funktionen
  • Große Argumente: Auf numerische Stabilität achten

Bessel-Funktionen - Vollständige Definitionen und Beziehungen

Gewöhnliche Bessel-Funktionen

Die Bessel-Funktion erster Art n-ter Ordnung ist definiert als:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Die Bessel-Funktion zweiter Art (Neumann-Funktion) ist:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]
Anwendungen der J-Funktionen

Gewöhnliche Bessel-Funktionen sind fundamental für alle oszillierenden Phänomene mit Zylindersymmetrie: Schwingungen von Trommelfellen, elektromagnetische Wellen in Hohlleitern, Quantenmechanik in zylindersymmetrischen Potentialen.

Modifizierte Bessel-Funktionen

Die modifizierte Bessel-Funktion erster Art ist definiert als:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

Die modifizierte Bessel-Funktion zweiter Art ist:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Hankel-Funktionen

Komplexe Linearkombinationen:
\(H_\nu^{(1)}(z) = J_\nu(z) + iY_\nu(z)\)
\(H_\nu^{(2)}(z) = J_\nu(z) - iY_\nu(z)\)

Wichtig für auslaufende und einlaufende Zylinderwellen.


Weitere Komplexe Funktionen

Betrag / Absolutwert • Division • Exponent • Konjugierte • Logarithmus zur Basis 10 • Multiplikation • Natürlicher Logarithmus • Polarform • Quadratwurzel • Wurzel • Potenz • Reziprok • Winkel •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy Funktion • Abgeleitete Airy Funktion •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye