Bessel-Y Function for Complex Numbers

Calculation of the Bessel function \(Y_\nu(z)\) of the second kind (Neumann function) with oscillatory behavior

Bessel-Y Function Calculator

Bessel Function \(Y_\nu(z)\) of the Second Kind

The Bessel function of the second kind \(Y_\nu(z)\) (also called Neumann function) exhibits oscillatory behavior and is singular at the origin. It is a linearly independent solution of the Bessel differential equation.

Complex Argument z = a + bi
+
i
Integer or rational order of the Bessel function
Calculation Result
\(Y_\nu(z)\) =

Bessel-Y Properties

Behavior

Oscillatory

Similar to \(J_\nu\)

Wave function
Origin

Singular

At z = 0

\(Y_\nu(0) = -\infty\)
Order

ν ∈ ℝ

Any real number

Integer or rational
Argument

z ∈ ℂ

Complex: a+bi

Real and imaginary part
Important Properties
  • Solution of the Bessel differential equation
  • Linearly independent from \(J_\nu(z)\)
  • Singularity: \(Y_0(z) \sim \frac{2}{\pi}\ln(z)\) for small z
  • Asymptotically: \(Y_\nu(z) \sim \sqrt{\frac{2}{\pi z}} \sin(z - \frac{\nu\pi}{2} - \frac{\pi}{4})\)
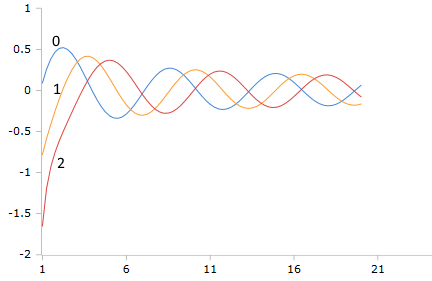
BesselY

Plot of the Bessel-Y function with orders 0, 1, and 2

Definition of the Bessel-Y Function (Neumann Function)

The Bessel function of the second kind \(Y_\nu(z)\), also called Neumann function or Weber function, is defined by:

Standard Definition
\[Y_\nu(z) = \frac{J_\nu(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Definition through the Bessel functions of the first kind \(J_\nu(z)\) and \(J_{-\nu}(z)\)

Bessel Differential Equation
\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} + (z^2 - \nu^2)w = 0\]

Differential equation with solutions \(w = J_\nu(z)\) and \(w = Y_\nu(z)\)

Wronskian Determinant
\[W[J_\nu, Y_\nu] = J_\nu Y_\nu' - J_\nu' Y_\nu = \frac{2}{\pi z}\]

Proof of linear independence

Important Properties of the Bessel-Y Function

Asymptotic Behavior
\[Y_\nu(z) \sim \sqrt{\frac{2}{\pi z}} \sin\left(z - \frac{\nu\pi}{2} - \frac{\pi}{4}\right)\]

Oscillatory for large |z| with decreasing amplitude

Behavior at Origin
\[Y_0(z) \sim \frac{2}{\pi} \ln(z)\] \[Y_\nu(z) \sim -\frac{\Gamma(\nu)}{\pi}\left(\frac{2}{z}\right)^\nu \text{ for } \nu > 0\]

Logarithmic or power singularity at origin

Symmetry Relations
\[Y_{-n}(z) = (-1)^n Y_n(z) \quad \text{for integer } n\]

Symmetry for integer orders

Recurrence Relations
\[Y_{\nu-1}(z) + Y_{\nu+1}(z) = \frac{2\nu}{z} Y_\nu(z)\] \[Y_{\nu-1}(z) - Y_{\nu+1}(z) = 2 Y_\nu'(z)\]

Relationships between different orders

Calculation Example: \(Y_1(2+i)\)
Given: z = 2 + i, ν = 1
Calculation: \(Y_1(z)\) via the definition:
\(Y_1(z) = \frac{J_1(z) \cos(\pi) - J_{-1}(z)}{\sin(\pi)}\)
Limit consideration: For integer ν, L'Hospital's rule is applied
\(Y_n(z) = \lim_{\nu \to n} \frac{J_\nu(z) \cos(\nu\pi) - J_{-\nu}(z)}{\sin(\nu\pi)}\)
Numerical result: \(Y_1(2+i)\) is complex with real and imaginary parts
Peculiarity: Singular at origin, oscillatory for large arguments

Applications of the Bessel-Y Function

Wave Propagation
Cylindrical waves Exterior solutions Radiation problems Scattering
Acoustics & Vibrations
Membranes:
Circular plates
Boundary value problems
Resonators:
Hollow cylinders
External fields
Electromagnetism

Waveguides

Antennas

Far-field patterns

Mathematical Physics

Potential theory

Green's functions

Boundary value problems

Integral transforms

Bessel-Y Functions (Neumann Functions) - Detailed Description

Oscillatory Behavior with Singularity

The Bessel function of the second kind \(Y_\nu(z)\) is a second, linearly independent solution of the Bessel differential equation. Unlike \(J_\nu(z)\), it is singular at the origin.

Characteristic Properties:
• Oscillatory behavior like \(J_\nu(z)\)
• Singularity at origin (z=0)
• Linearly independent from \(J_\nu(z)\)
• Complete basis with \(J_\nu\) for boundary value problems

Historical Background

The function was independently developed by Carl Neumann and Heinrich Martin Weber. It is therefore also called Neumann function \(N_\nu(z)\) or Weber function.

Physical Interpretation

In exterior problems, \(Y_\nu(r)\) often describes the outgoing wave in the far field, while \(J_\nu(r)\) represents the incoming or standing wave. The combination \(H_\nu^{(1)} = J_\nu + iY_\nu\) forms the Hankel function for outgoing waves.

Numerical Aspects

The calculation of \(Y_\nu(z)\) requires special care due to the singularity at the origin and the oscillatory behavior for large arguments.

Numerical Properties:
• Caution near z=0 due to singularity
• Recurrence can be unstable
• Better stability backward
• Asymptotic expansion for large |z|

Calculation Methods

Different numerical methods are used depending on the argument range:

Small |z|: Series expansion (with singularity)
Medium |z|: Miller algorithm
Large |z|: Asymptotic expansion
Complex z: Special algorithms required

Relationship to Other Functions

Hankel functions:
\(H_\nu^{(1)}(z) = J_\nu(z) + iY_\nu(z)\) (outgoing wave)
\(H_\nu^{(2)}(z) = J_\nu(z) - iY_\nu(z)\) (incoming wave)

Comparison: Bessel-Y vs. Bessel-J

Bessel-Y Function (second kind)
Definition: \(Y_\nu(z)\) via \(J_{\pm\nu}(z)\)
Behavior: Oscillatory
Origin: Singular at z=0
Asymptotics: \(\sim \sqrt{\frac{2}{\pi z}} \sin(\cdots)\)
Application: Exterior problems
Bessel-J Function (first kind)
Definition: \(J_\nu(z)\) via series
Behavior: Oscillatory
Origin: Finite at z=0
Asymptotics: \(\sim \sqrt{\frac{2}{\pi z}} \cos(\cdots)\)
Application: Interior problems
Application Guidelines
  • Exterior problems: Combination \(J_\nu\) + \(Y_\nu\)
  • Boundary values at z→∞: Hankel functions \(H_\nu^{(1,2)}\)
  • Wave radiation: \(Y_\nu\) for outgoing waves
  • Interior problems: Only \(J_\nu\) (finite at z=0)
  • Singularity at boundary: \(Y_\nu\) allowed
  • Complete basis: Combination of both functions

Bessel Functions - Complete Definitions and Relationships

Ordinary Bessel Functions

The Bessel function of the first kind of order n is defined as:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

The Bessel function of the second kind (Neumann function) is:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]
Hankel Functions

Combinations of \(J_\nu\) and \(Y_\nu\) for wave problems:
\(H_\nu^{(1)}(z) = J_\nu(z) + iY_\nu(z)\) (outgoing wave)
\(H_\nu^{(2)}(z) = J_\nu(z) - iY_\nu(z)\) (incoming wave)

Modified Bessel Functions

The modified Bessel function of the first kind is:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

The modified Bessel function of the second kind is:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Application Areas

The Bessel-Y function is indispensable for exterior problems with cylindrical symmetry, where singularities at z=0 are allowed. It is used in wave theory, acústics, electromagnetism, and many other areas of mathematical physics.


More complex functions

Absolute value (abs) • Angle • Conjugate • Division • Exponent • Logarithm to base 10 • Multiplication • Natural logarithm • Polarform • Power • Root • Reciprocal • Square root •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy function • Derivative Airy function •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye •