Bessel-Y Funktion für komplexe Zahlen

Berechnung der Bessel-Funktion \(Y_\nu(z)\) der zweiten Art (Neumann-Funktion) mit oszillierendem Verhalten

Bessel-Y Funktionsrechner

Bessel-Funktion \(Y_\nu(z)\) zweiter Art

Die Bessel-Funktion zweiter Art \(Y_\nu(z)\) (auch Neumann-Funktion genannt) zeigt oszillierendes Verhalten und ist singulär am Ursprung. Sie ist eine linear unabhängige Lösung der Bessel-Differentialgleichung.

Komplexes Argument z = a + bi
+
i
Ganzzahlige oder rationale Ordnung der Bessel-Funktion
Berechnungsergebnis
\(Y_\nu(z)\) =

Bessel-Y Eigenschaften

Verhalten

Oszillierend

Ähnlich zu \(J_\nu\)

Wellenfunktion
Ursprung

Singulär

Bei z = 0

\(Y_\nu(0) = -\infty\)
Ordnung

ν ∈ ℝ

Beliebige reelle Zahl

Ganzzahlig oder rational
Argument

z ∈ ℂ

Komplex: a+bi

Reell- und Imaginärteil
Wichtige Eigenschaften
  • Lösung der Bessel-Differentialgleichung
  • Linear unabhängig zu \(J_\nu(z)\)
  • Singularität: \(Y_0(z) \sim \frac{2}{\pi}\ln(z)\) für kleine z
  • Asymptotisch: \(Y_\nu(z) \sim \sqrt{\frac{2}{\pi z}} \sin(z - \frac{\nu\pi}{2} - \frac{\pi}{4})\)
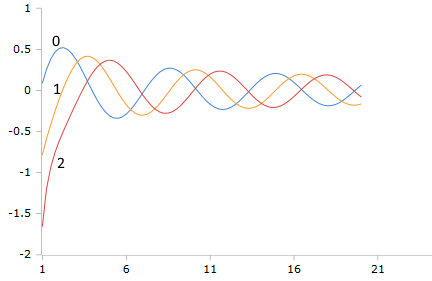
BesselY

Plot der Bessel-Y Funktion mit den Ordnungszahlen 0, 1 und 2

Definition der Bessel-Y Funktion (Neumann-Funktion)

Die Bessel-Funktion zweiter Art \(Y_\nu(z)\), auch Neumann-Funktion oder Weber-Funktion genannt, ist definiert durch:

Standarddefinition
\[Y_\nu(z) = \frac{J_\nu(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]

Definition durch die Bessel-Funktionen erster Art \(J_\nu(z)\) und \(J_{-\nu}(z)\)

Bessel-Differentialgleichung
\[z^2 \frac{d^2w}{dz^2} + z \frac{dw}{dz} + (z^2 - \nu^2)w = 0\]

Differentialgleichung mit Lösungen \(w = J_\nu(z)\) und \(w = Y_\nu(z)\)

Wronskische Determinante
\[W[J_\nu, Y_\nu] = J_\nu Y_\nu' - J_\nu' Y_\nu = \frac{2}{\pi z}\]

Beweis der linearen Unabhängigkeit

Wichtige Eigenschaften der Bessel-Y Funktion

Asymptotisches Verhalten
\[Y_\nu(z) \sim \sqrt{\frac{2}{\pi z}} \sin\left(z - \frac{\nu\pi}{2} - \frac{\pi}{4}\right)\]

Oszillierend für große |z| mit abnehmender Amplitude

Verhalten am Ursprung
\[Y_0(z) \sim \frac{2}{\pi} \ln(z)\] \[Y_\nu(z) \sim -\frac{\Gamma(\nu)}{\pi}\left(\frac{2}{z}\right)^\nu \text{ für } \nu > 0\]

Logarithmische bzw. Potenz-Singularität am Ursprung

Symmetrierelationen
\[Y_{-n}(z) = (-1)^n Y_n(z) \quad \text{für ganzzahlige } n\]

Symmetrie für ganzzahlige Ordnungen

Rekurrenzrelationen
\[Y_{\nu-1}(z) + Y_{\nu+1}(z) = \frac{2\nu}{z} Y_\nu(z)\] \[Y_{\nu-1}(z) - Y_{\nu+1}(z) = 2 Y_\nu'(z)\]

Beziehungen zwischen verschiedenen Ordnungen

Berechnungsbeispiel: \(Y_1(2+i)\)
Gegeben: z = 2 + i, ν = 1
Berechnung: \(Y_1(z)\) über die Definition:
\(Y_1(z) = \frac{J_1(z) \cos(\pi) - J_{-1}(z)}{\sin(\pi)}\)
Grenzwertbetrachtung: Für ganzzahlige ν wird L'Hospital angewendet
\(Y_n(z) = \lim_{\nu \to n} \frac{J_\nu(z) \cos(\nu\pi) - J_{-\nu}(z)}{\sin(\nu\pi)}\)
Numerisches Ergebnis: \(Y_1(2+i)\) ist komplex mit Real- und Imaginärteil
Besonderheit: Singulär am Ursprung, oszillierend für große Argumente

Anwendungen der Bessel-Y Funktion

Wellenausbreitung
Zylinderwellen Außenraumlösungen Abstrahlprobleme Streuung
Akustik & Schwingungen
Membranen:
Kreisförmige Platten
Randwertprobleme
Resonatoren:
Hohlzylinder
Außenfelder
Elektromagnetik

Wellenleiter

Antennen

Fernfeld-Muster

Mathematische Physik

Potentialtheorie

Greensche Funktionen

Randwertprobleme

Integraltransformen

Bessel-Y Funktionen (Neumann-Funktionen) - Detaillierte Beschreibung

Oszillierendes Verhalten mit Singularität

Die Bessel-Funktion zweiter Art \(Y_\nu(z)\) ist eine zweite, linear unabhängige Lösung der Bessel-Differentialgleichung. Im Gegensatz zu \(J_\nu(z)\) ist sie am Ursprung singulär.

Charakteristische Eigenschaften:
• Oszillierendes Verhalten wie \(J_\nu(z)\)
• Singularität am Ursprung (z=0)
• Linear unabhängig zu \(J_\nu(z)\)
• Vollständige Basis mit \(J_\nu\) für Randwertprobleme

Historischer Hintergrund

Die Funktion wurde von Carl Neumann und Heinrich Martin Weber unabhängig entwickelt. Sie wird daher auch Neumann-Funktion \(N_\nu(z)\) oder Weber-Funktion genannt.

Physikalische Interpretation

In Außenraumproblemen beschreibt \(Y_\nu(r)\) oft die ausgehende Welle im Fernfeld, während \(J_\nu(r)\) die eingehende oder stehende Welle darstellt. Die Kombination \(H_\nu^{(1)} = J_\nu + iY_\nu\) bildet die Hankel-Funktion für ausgehende Wellen.

Numerische Aspekte

Die Berechnung von \(Y_\nu(z)\) erfordert besondere Sorgfalt wegen der Singularität am Ursprung und des oszillierenden Verhaltens bei großen Argumenten.

Numerische Eigenschaften:
• Vorsicht nahe z=0 wegen Singularität
• Rekurrenz kann instabil sein
• Bessere Stabilität rückwärts
• Asymptotische Entwicklung für große |z|

Berechnungsmethoden

Verschiedene numerische Methoden werden je nach Argumentbereich verwendet:

Kleine |z|: Reihenentwicklung (mit Singularität)
Mittlere |z|: Miller-Algorithmus
Große |z|: Asymptotische Entwicklung
Komplexe z: Spezielle Algorithmen erforderlich

Beziehung zu anderen Funktionen

Hankel-Funktionen:
\(H_\nu^{(1)}(z) = J_\nu(z) + iY_\nu(z)\) (ausgehende Welle)
\(H_\nu^{(2)}(z) = J_\nu(z) - iY_\nu(z)\) (eingehende Welle)

Vergleich: Bessel-Y vs. Bessel-J

Bessel-Y Funktion (zweite Art)
Definition: \(Y_\nu(z)\) über \(J_{\pm\nu}(z)\)
Verhalten: Oszillierend
Ursprung: Singulär bei z=0
Asymptotik: \(\sim \sqrt{\frac{2}{\pi z}} \sin(\cdots)\)
Anwendung: Außenraumprobleme
Bessel-J Funktion (erste Art)
Definition: \(J_\nu(z)\) via Reihe
Verhalten: Oszillierend
Ursprung: Endlich bei z=0
Asymptotik: \(\sim \sqrt{\frac{2}{\pi z}} \cos(\cdots)\)
Anwendung: Innenraumprobleme
Anwendungsrichtlinien
  • Außenraumprobleme: Kombination \(J_\nu\) + \(Y_\nu\)
  • Randwerte bei z→∞: Hankel-Funktionen \(H_\nu^{(1,2)}\)
  • Wellenabstrahlung: \(Y_\nu\) für ausgehende Wellen
  • Innenraumprobleme: Nur \(J_\nu\) (endlich bei z=0)
  • Singularität am Rand: \(Y_\nu\) erlaubt
  • Vollständige Basis: Kombination beider Funktionen

Bessel-Funktionen - Vollständige Definitionen und Beziehungen

Gewöhnliche Bessel-Funktionen

Die Bessel-Funktion erster Art n-ter Ordnung ist definiert als:

\[J_{\nu}(z) = \sum_{m=0}^{\infty} \frac{(-1)^m}{m! \Gamma(m + \nu + 1)} \left(\frac{z}{2}\right)^{2m + \nu}\]

Die Bessel-Funktion zweiter Art (Neumann-Funktion) ist:

\[Y_{\nu}(z) = \frac{J_{\nu}(z) \cos(\nu \pi) - J_{-\nu}(z)}{\sin(\nu \pi)}\]
Hankel-Funktionen

Kombinationen von \(J_\nu\) und \(Y_\nu\) für Wellenproblem:
\(H_\nu^{(1)}(z) = J_\nu(z) + iY_\nu(z)\) (ausgehende Welle)
\(H_\nu^{(2)}(z) = J_\nu(z) - iY_\nu(z)\) (eingehende Welle)

Modifizierte Bessel-Funktionen

Die modifizierte Bessel-Funktion erster Art ist:

\[I_{\nu}(z) = i^{-\nu} J_{\nu}(iz)\]

Die modifizierte Bessel-Funktion zweiter Art ist:

\[K_{\nu}(z) = \frac{\pi}{2} \frac{I_{-\nu}(z) - I_{\nu}(z)}{\sin(\nu \pi)}\]
Anwendungsgebiete

Die Bessel-Y Funktion ist unverzichtbar für Außenraumprobleme mit Zylindersymmetrie, wo Singularitäten bei z=0 erlaubt sind. Sie wird in der Wellentheorie, Akustik, Elektromagnetik und vielen anderen Bereichen der mathematischen Physik verwendet.


Weitere Komplexe Funktionen

Betrag / Absolutwert • Division • Exponent • Konjugierte • Logarithmus zur Basis 10 • Multiplikation • Natürlicher Logarithmus • Polarform • Quadratwurzel • Wurzel • Potenz • Reziprok • Winkel •
Cosh • Sinh • Tanh •
Acos • Asin • Atan • Cos • Sin • Tan •
Airy Funktion • Abgeleitete Airy Funktion •
Bessel-I • Bessel-Ie • Bessel-J • Bessel-Je • Bessel-K • Bessel-Ke • Bessel-Y • Bessel-Ye