Cube Calculator
Online calculator and formulas for calculating the volume, surface area and diagonal of a cube
Cube Calculator
The Regular Cube
A cube (regular hexahedron) is a platonic solid with six square faces and edges of equal length.
Platonic Solid Properties
The Regular Hexahedron: One of the five perfect platonic solids
Cube Structure
The perfect cube with equal edges and right angles.
The most fundamental 3D shape.
|
|
What is a Cube?
A cube (regular hexahedron) is one of the five platonic solids:
- Definition: Six congruent square faces
- Platonic Solid: Perfect regular polyhedron
- Faces: 6 identical squares
- Vertices: 8 corners
- Edges: 12 equal edges
- Symmetry: Perfect Oh symmetry
Geometric Properties of the Cube
The cube demonstrates the most fundamental geometric properties:
Basic Parameters
- Faces: 6 congruent squares
- Vertices: 8 corners (all identical)
- Edges: 12 edges (all equal length)
- Euler characteristic: V - E + F = 8 - 12 + 6 = 2
Special Properties
- Right angles: All face angles are 90°
- Equal edges: All 12 edges are identical
- Regular faces: All faces are squares
- Convex: No inward-pointing edges or vertices
Mathematical Relationships
The cube follows elegant and simple mathematical relationships:
Volume Formula
Simple cubic relationship. Fundamental and elegant.
Surface Formula
Six identical square faces. Simple multiplication by 6.
Applications of the Cube
Cubes are found everywhere in nature, technology, and human design:
Architecture & Construction
- Building foundations and structures
- Modular construction systems
- Storage containers and boxes
- Architectural design elements
Science & Technology
- Crystal structures (salt, metals)
- Computer graphics and 3D modeling
- Engineering components
- Packaging and manufacturing
Education & Learning
- Basic geometry instruction
- 3D spatial reasoning development
- Mathematical concept visualization
- Volume and area calculations
Art & Design
- Minimalist sculptures and art
- Industrial design
- Furniture and product design
- Gaming dice and puzzles
Cube Formulas
Volume (V)
Simple cubic relationship - the most fundamental volume formula
Surface Area (S)
Six identical square faces
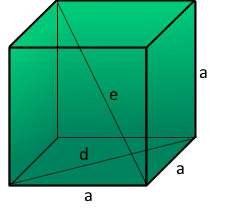
Face Diagonal (d)
Diagonal across a square face using Pythagorean theorem
Space Diagonal (e)
Diagonal through the center of the cube
Inverse Formulas (from given parameters)
\(a = \sqrt[3]{V}\)
\(a = \sqrt{\frac{S}{6}}\)
\(a = \frac{d}{\sqrt{2}}\)
\(a = \frac{e}{\sqrt{3}}\)
All cube properties can be calculated from any single parameter
Calculation Example for a Cube
Given
Find: All properties of the cube
1. Volume Calculation
For a = 5:
\[V = 5^3\] \[V = 125\]The volume is 125 cubic units
2. Surface Area Calculation
For a = 5:
\[S = 6 \cdot 5^2\] \[S = 6 \cdot 25 = 150\]The surface area is 150 square units
3. Face Diagonal Calculation
For a = 5:
\[d = \sqrt{2} \cdot 5\] \[d \approx 1.414 \cdot 5 = 7.07\]The face diagonal is approximately 7.07 units
4. Space Diagonal Calculation
For a = 5:
\[e = \sqrt{3} \cdot 5\] \[e \approx 1.732 \cdot 5 = 8.66\]The space diagonal is approximately 8.66 units
5. Complete Cube Properties
The perfect cube with fundamental geometric relationships
The Cube: Foundation of 3D Geometry
The cube is the most fundamental three-dimensional shape, serving as the cornerstone of geometric understanding. As one of the five Platonic solids, it represents perfect geometric harmony with its six congruent square faces, eight identical vertices, and twelve equal edges. The mathematical beauty of the cube lies in its simplicity and elegance - from the straightforward cubic relationship for volume to the elegant square root relationships for its diagonals. This perfect regularity makes the cube an ideal foundation for understanding spatial relationships, coordinate systems, and the principles of three-dimensional geometry.
The Geometry of Perfect Order
The cube exemplifies geometric perfection and mathematical order:
- Platonic Solid: One of only five perfectly regular 3D shapes
- Oh Symmetry: The highest possible 3D symmetry group
- Orthogonal: All edges meet at perfect right angles
- Regular Faces: Six identical square faces
- Equal Edges: All twelve edges have identical length
- Spatial Foundation: Basis for Cartesian coordinate systems
- Universal Application: Found throughout nature, technology, and art
Mathematical Elegance
Simplicity of Relationships
The cube's formulas are elegantly simple, with volume as a³, surface as 6a², and diagonals involving √2 and √3 - the most fundamental mathematical constants.
Fundamental Constants
The cube naturally incorporates √2 and √3, connecting it to the most basic geometric and algebraic relationships in mathematics.
Geometric Foundation
As the basis for cubic lattices, coordinate systems, and modular design, the cube serves as the foundation for countless applications.
Universal Presence
From crystal structures to architecture, from computer graphics to packaging, the cube appears everywhere due to its optimal properties.
Summary
The cube stands as the ultimate expression of geometric perfection and mathematical elegance. Its simple yet profound relationships - from the basic cubic volume formula to the elegant diagonal relationships involving √2 and √3 - make it both a fundamental teaching tool and a practical foundation for countless applications. As a Platonic solid with perfect Oh symmetry, the cube represents the harmony between mathematical theory and practical utility. From ancient Greek geometry to modern computer graphics, from crystal structures to architectural design, the cube continues to demonstrate that the most profound mathematical truths are often found in the simplest forms. Its universal presence in both nature and human design testifies to the power and beauty of perfect geometric relationships.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron