Right Wedge Calculator
Online calculator and formulas for calculating a right wedge
Right Wedge Calculator
The Right Wedge
A Right Wedge is a pentahedral solid with a triangular cross-section and straight vertical edges.
Right Wedge Properties
The pentahedral wedge: Five faces with triangular cross-section
Right Wedge Structure
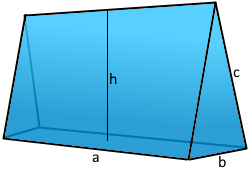
The right wedge with triangular cross-section.
Perfect for splitting and cutting applications.
|
|
What is a Right Wedge?
A Right Wedge is a distinctive 3D geometric solid:
- Definition: A pentahedral solid with triangular cross-section
- Five faces: Two triangular and three rectangular faces
- Right angles: Vertical edges perpendicular to base
- Vertices: 6 vertices total
- Edges: 9 edges (3 + 3 + 3)
- Applications: Splitting, cutting, and mechanical tools
Geometric Properties of Right Wedges
The Right Wedge demonstrates practical geometric properties:
Basic Parameters
- Faces: 2 triangular, 3 rectangular
- Base: Rectangular with dimensions a × b
- Height: Perpendicular distance from base
- Euler formula: V - E + F = 6 - 9 + 5 = 2
Special Properties
- Right angles: Vertical edges at 90° to base
- Triangular taper: Linear reduction to edge
- Mechanical advantage: Force concentration
- Splitting efficiency: Optimal wedge geometry
Mathematical Relationships
The Right Wedge follows fundamental geometric principles:
Volume Formula
Simple formula: half the rectangular base area times height. Elegant and practical.
Surface Formula
Base plus three rectangular faces. Accounts for all surface area.
Applications of Right Wedges
Right Wedges have numerous practical applications:
Tools & Machinery
- Splitting wedges and mauls
- Cutting tools and chisels
- Press and forming dies
- Mechanical separators
Construction & Engineering
- Structural support elements
- Architectural details
- Foundation wedges
- Bridge and beam supports
Forestry & Agriculture
- Log splitting wedges
- Tree felling wedges
- Agricultural implements
- Harvesting tools
Education & Physics
- Simple machine demonstrations
- Force multiplication studies
- Geometry teaching models
- Engineering design examples
Right Wedge Formulas
Volume (V)
Half the base area times height
Surface Area (S)
Base plus three rectangular faces
Side Length (c)
Slant edge using Pythagorean theorem
Height (h)
Height from slant edge and base
Right Wedge Parameters
Base length
Base width
Vertical height
Diagonal edge
The right wedge tapers linearly from the rectangular base to a line edge
Calculation Example for a Right Wedge
Given
Find: Height and all properties of the right wedge
1. Height Calculation
Using the height formula:
\[h = \sqrt{c^2 - \left( \frac{b}{2} \right)^2}\] \[h = \sqrt{4^2 - \left( \frac{5}{2} \right)^2}\] \[h = \sqrt{16 - 6.25}\] \[h = \sqrt{9.75} ≈ 3.12\]The height is approximately 3.12 units
2. Volume Calculation
Using the volume formula:
\[V = \frac{a \cdot b \cdot h}{2}\] \[V = \frac{10 \cdot 5 \cdot 3.12}{2}\] \[V = \frac{156}{2} = 78\]The volume is 78 cubic units
3. Surface Area Calculation
Using the surface area formula:
\[S = a \cdot b + 2 \cdot a \cdot c + h \cdot b\] \[S = 10 \cdot 5 + 2 \cdot 10 \cdot 4 + 3.12 \cdot 5\] \[S = 50 + 80 + 15.6 = 145.6\]The surface area is 145.6 square units
4. Complete Right Wedge Properties
The right wedge with optimal splitting geometry
The Right Wedge: The Perfect Splitting Tool
The Right Wedge represents one of humanity's most enduring and practical geometric innovations. As one of the six classical simple machines, the wedge demonstrates how geometric principles can be harnessed to multiply force and accomplish work that would otherwise be impossible. With its distinctive pentahedral form—five faces that taper from a rectangular base to a linear edge—the right wedge embodies both mathematical elegance and mechanical efficiency. From ancient stone-cutting tools to modern industrial applications, this geometric form continues to serve as an essential bridge between theoretical mathematics and practical problem-solving.
The Mechanics of Force Multiplication
The Right Wedge demonstrates fundamental mechanical principles:
- Force concentration: Distributes applied force over smaller area
- Mechanical advantage: Input force multiplied by geometry
- Right angle precision: Vertical edges ensure proper force direction
- Triangular taper: Linear reduction maximizes splitting efficiency
- Surface optimization: Minimal surface area for maximum effect
- Pythagorean relationships: Height and slant connected by theorem
- Pentahedral structure: Five faces provide stability and function
Engineering Excellence
Simple Machine Mastery
The right wedge exemplifies how simple geometric principles can create powerful mechanical advantage, transforming small forces into large splitting forces.
Mathematical Precision
The wedge's formulas beautifully demonstrate relationships between base dimensions, height, and slant edges using fundamental geometric principles.
Practical Applications
From log splitting to stone cutting, the right wedge's geometry has been optimized over millennia for maximum efficiency in separating materials.
Timeless Design
The wedge's form factor remains essentially unchanged because its geometry represents an optimal solution to the force multiplication problem.
Summary
The Right Wedge stands as a testament to the power of applied geometry in solving practical human challenges. Its pentahedral form, with two triangular and three rectangular faces, creates an optimal balance between mechanical advantage and structural integrity. The mathematical relationships governing its dimensions—from the simple volume formula to the Pythagorean connections between height and slant—reveal the elegant principles underlying this ancient tool. Whether encountered in a physics classroom as an example of simple machines, in a workshop as a splitting tool, or in an engineering context as a force multiplier, the right wedge continues to demonstrate how mathematical precision can be translated into mechanical power. In an age of complex technology, the wedge reminds us that sometimes the most profound solutions are also the most geometrically simple.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron