Pentagonal Trapezohedron Calculator
Calculator and formulas for a pentagonal trapezohedron
Pentagonal Trapezohedron Calculator
The Pentagonal Trapezohedron
A pentagonal trapezohedron is a twisted double pyramid with 10 kite-shaped faces, rotated by 36°.
Pentagonal Trapezohedron Properties
The twisted double pyramid: Golden ratio relationships throughout
Trapezohedron Structure
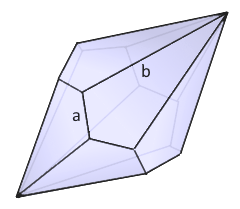
The twisted double pyramid with kite faces.
Rotation by 36° creates the twist.
|
|
What is a Pentagonal Trapezohedron?
A pentagonal trapezohedron is a remarkable geometric solid:
- Definition: Twisted double pyramid (deltohedron)
- Faces: 10 congruent kite-shaped faces
- Twist angle: 36° rotation (180°/5)
- Vertices: 16 vertices (2 polar + 14 equatorial)
- Edges: 24 edges (10 short a + 10 long b + 4 polar)
- Golden ratio: All dimensions relate to φ
Geometric Properties of the Pentagonal Trapezohedron
The pentagonal trapezohedron exhibits fascinating geometric properties:
Basic Structure
- Dual polyhedron: Dual of pentagonal antiprism
- Face type: All faces are congruent kites
- Euler formula: V - E + F = 16 - 24 + 10 = 2
- Symmetry: D₅d dihedral symmetry
Golden Ratio Magic
- Edge ratio: b/a = φ (golden ratio)
- Self-similarity: Scaling properties
- Pentagon connection: Related to regular pentagon
- Natural occurrence: Appears in crystals
Mathematical Relationships
The pentagonal trapezohedron follows elegant golden ratio laws:
Volume Formula
Golden ratio embedded in volume. Elegant mathematical relationship.
Surface Formula
Sum of 10 kite areas. Based on golden ratio geometry.
Applications of Pentagonal Trapezohedra
Pentagonal trapezohedra find applications in various fields:
Gaming & Recreation
- 10-sided dice (d10)
- Role-playing games
- Probability experiments
- Educational models
Science & Crystallography
- Crystal formations
- Mineralogy studies
- Molecular geometry
- Structural analysis
Education & Mathematics
- Golden ratio demonstrations
- 3D geometry teaching
- Symmetry studies
- Mathematical modeling
Art & Design
- Sculptural works
- Architectural elements
- Decorative objects
- Geometric art
Pentagonal Trapezohedron Formulas
Edge a (Short Edge)
Short edge relates to antiprism parameter z
Edge b (Long Edge)
Long edge equals golden ratio times z
Height (h)
Height with nested radical involving √5
Surface (S)
Surface area of 10 kite faces
Volume (V)
Volume with golden ratio factor
Golden Ratio φ
The golden ratio appearing throughout
Trapezohedron Parameters
10 congruent kites
16 vertices
24 edges total
36° rotation
All properties are based on the antiprism parameter z and the golden ratio φ
Calculation Example for a Pentagonal Trapezohedron
Given
Find: All properties of the pentagonal trapezohedron
1. Edge Calculations
Short edge a:
\[a = \frac{\sqrt{5}-1}{2} \cdot 10 = \frac{1.236}{2} \cdot 10 \approx 6.18\]Long edge b:
\[b = \frac{\sqrt{5}+1}{2} \cdot 10 = \frac{3.236}{2} \cdot 10 \approx 16.18\]Perfect golden ratio relationship: b/a = φ
2. Height & Volume
Height h:
\[h = \sqrt{5 + 2\sqrt{5}} \cdot 10 \approx 3.078 \cdot 10 = 30.78\]Volume V:
\[V = \frac{5(3+\sqrt{5})}{12} \cdot 1000 \approx 2182\]Height and volume with golden ratio factors
3. Complete Pentagonal Trapezohedron (z = 10)
A perfect pentagonal trapezohedron with golden ratio proportions
The Pentagonal Trapezohedron: Golden Ratio in 3D
The pentagonal trapezohedron is a mathematical marvel that brings the golden ratio into three-dimensional space. As the dual polyhedron of the pentagonal antiprism, it consists of 10 congruent kite-shaped faces arranged around two pentagonal "caps." What makes this solid extraordinary is that every dimension - from edge lengths to volume - is intimately connected to the golden ratio φ = (1+√5)/2 ≈ 1.618, creating a perfect harmony between mathematical beauty and geometric functionality.
The Golden Ratio Connection
The pentagonal trapezohedron demonstrates the golden ratio's omnipresence:
- Edge ratio: The long edge b is exactly φ times the short edge a
- Pentagon relationship: Derived from the regular pentagon's geometry
- Self-similarity: Scaling properties maintain golden proportions
- Dual structure: Dual of pentagonal antiprism with twist angle 36°
- Crystal formation: Natural occurrence in pyrite and other minerals
- Gaming applications: Perfect shape for 10-sided dice (d10)
- Aesthetic appeal: Pleasing proportions in art and design
Mathematical Elegance
Nested Radicals
The formulas feature beautiful nested radicals involving √5, creating elegant mathematical expressions that all trace back to the golden ratio.
Symmetry Properties
The D₅d dihedral symmetry group provides rich symmetry properties, making it ideal for both mathematical study and practical applications.
Crystallographic Importance
This shape appears naturally in crystal structures, particularly in pyrite formations, demonstrating nature's preference for golden ratio geometries.
Gaming Perfect
The 10 equivalent faces make it the ideal shape for a fair 10-sided die, combining mathematical perfection with practical functionality.
Summary
The pentagonal trapezohedron stands as a testament to the profound connections between the golden ratio and three-dimensional geometry. From its role as the ubiquitous d10 die in gaming to its appearance in natural crystal formations, this polyhedron bridges the gap between abstract mathematical beauty and tangible reality. Its elegant formulas, all rooted in the golden ratio and √5, demonstrate how a simple geometric transformation - the twisting of a double pyramid - can create a shape of remarkable mathematical richness. Whether studied for its crystallographic properties, admired for its aesthetic proportions, or utilized for its practical gaming applications, the pentagonal trapezohedron remains one of geometry's most fascinating and useful forms.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron