Prismatoid Calculator
Calculator and formulas for a prismatoid
Prismatoid Calculator
The Prismatoid
A Prismatoid is a geometric solid with variable parallel polygonal faces and triangular/trapezoidal sides.
Prismatoid Properties
The flexible solid: Different parallel faces connected by triangular/trapezoidal sides
Prismatoid Structure
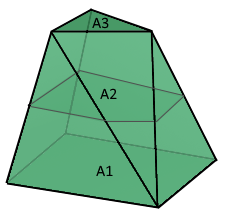
The variable geometric solid with different parallel faces.
Connected by triangular or trapezoidal sides.
|
|
What is a Prismatoid?
A Prismatoid is a fascinating geometric solid:
- Definition: Solid with parallel polygonal base and top
- Variable faces: Base and top can be different shapes/sizes
- Side faces: Triangles, trapezoids, or parallelograms
- Flexibility: Bases don't need to be congruent
- Variety: Different number of corners allowed
- Formula: Uses Simpson's 1/3 rule
Geometric Properties of Prismatoids
The Prismatoid demonstrates remarkable geometric flexibility:
Basic Parameters
- Base faces: Two parallel polygons (can differ)
- Side faces: Triangles, trapezoids, parallelograms
- Cross-section: Varies linearly with height
- Volume formula: Simpson's 1/3 rule
Special Properties
- Geometric flexibility: Variable face shapes
- Linear variation: Smooth transition between faces
- Integration principle: Based on numerical integration
- Versatile form: Includes prisms and pyramids as special cases
Mathematical Relationships
The Prismatoid follows the elegant Simpson's rule:
Volume Formula
Uses three areas: base, middle cross-section, and top. Accurate and elegant.
Integration Principle
Approximates the integral of area function. Highly accurate method.
Applications of Prismatoids
Prismatoids find applications in various fields:
Civil Engineering
- Earthwork volume calculations
- Dam and embankment design
- Road construction
- Tunnel excavation volumes
Manufacturing & Design
- Container and tank design
- Material volume calculations
- Architectural elements
- Product packaging
Education & Research
- Numerical integration teaching
- Volume approximation methods
- Calculus applications
- Engineering mathematics
Science & Analysis
- Geological volume estimates
- Fluid mechanics
- Environmental modeling
- Statistical analysis
Prismatoid Formula
Volume (V) - Simpson's 1/3 Rule
Volume using three cross-sectional areas
Height from Volume
Calculate height when volume is known
Parameter Meaning
A₂: Middle cross-section area
A₃: Top area
h: Height of the prismatoid
All areas measured perpendicular to height
Simpson's Rule Explanation
The prismatoid formula is based on Simpson's 1/3 rule for numerical integration. It provides an exact result for any prismatoid by using three equally spaced cross-sectional areas: the base (A₁), the middle section (A₂), and the top (A₃). The formula weights the middle area by factor 4, giving it greater influence in the volume calculation. This method is particularly accurate because it can exactly integrate polynomials up to degree 3, making it perfect for prismatoids where the cross-sectional area varies as a quadratic function of height.
Calculation Example for a Prismatoid
Given
Find: Volume of the prismatoid
1. Apply Simpson's Formula
Using the prismatoid formula:
\[V = \frac{h}{6} \cdot ( A_1 + 4A_2 + A_3 )\] \[V = \frac{20}{6} \cdot ( 5 + 4 \cdot 6 + 8 )\] \[V = \frac{20}{6} \cdot ( 5 + 24 + 8 )\]Substitute the known values into the formula
2. Calculate the Result
Continue the calculation:
\[V = \frac{20}{6} \cdot 37\] \[V = 3.333... \cdot 37\] \[V ≈ 123.33\]The volume is approximately 123.33 cubic units
3. Understanding the Result
The prismatoid demonstrates the power of Simpson's 1/3 rule for volume calculation
The Prismatoid: The Variable Geometric Solid
The Prismatoid represents one of the most versatile and practically important geometric solids in mathematics and engineering. Unlike rigid forms such as prisms where all cross-sections are identical, the prismatoid allows for variable cross-sections, making it ideal for modeling real-world objects and structures. The elegance of the prismatoid lies not only in its geometric flexibility but also in the mathematical sophistication of its volume formula, which is based on Simpson's 1/3 rule—one of the most fundamental principles of numerical integration.
The Mathematics of Flexibility
The Prismatoid demonstrates the beauty of variable geometry:
- Variable cross-sections: Linear change in area with height
- Simpson's rule: Exact integration using three points
- Weighted averaging: Middle section gets 4× weight
- Polynomial exactness: Perfect for cubic area functions
- Geometric generality: Includes prisms and pyramids as special cases
- Practical accuracy: Excellent approximation for complex shapes
- Engineering utility: Essential for earthwork and volume calculations
Mathematical Elegance
Simpson's Legacy
The prismatoid formula showcases the power of Simpson's 1/3 rule, demonstrating how numerical integration principles can provide exact solutions for geometric problems.
Practical Precision
The weighted middle section (4A₂) captures the curvature of the area function, providing remarkable accuracy with minimal data points.
Engineering Applications
From earthwork calculations to container design, the prismatoid's flexibility makes it indispensable in practical engineering applications.
Mathematical Foundation
The prismatoid bridges pure mathematics and applied engineering, showing how integration theory solves real-world volume problems.
Summary
The Prismatoid stands as a testament to the power of mathematical flexibility in geometric modeling. Its ability to handle variable cross-sections through the elegant Simpson's 1/3 rule makes it invaluable for engineers, architects, and scientists who need to calculate volumes of irregular solids. From ancient earthwork calculations to modern architectural design, the prismatoid continues to serve as a bridge between theoretical mathematics and practical problem-solving. Its formula may be simple, but its applications are limitless, demonstrating how the marriage of geometric intuition and numerical integration can solve complex real-world challenges with remarkable precision and elegance.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron