Oblique Prism Calculator
Calculator and formulas for an oblique prism
Oblique Prism Calculator
The Oblique Prism
An oblique prism is a slanted prismatic solid where the top surface is shifted horizontally, creating parallelogram side faces.
Oblique Prism Properties
The slanted prism: Top surface shifted horizontally creating parallelogram sides
Oblique Prism Structure
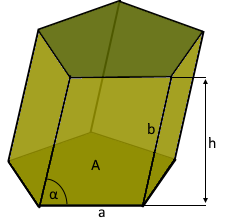
The prism with shifted parallel bases.
Creates parallelogram side faces.
|
|
What is an Oblique Prism?
An oblique prism represents a fascinating variation of the traditional prism:
- Definition: Prism with shifted parallel bases
- Top surface: Horizontally shifted relative to base
- Side faces: Parallelograms instead of rectangles
- Volume: Same as right prism (Cavalieri's principle)
- Angle: Characterized by oblique angle α
- Applications: Architecture and engineering
Geometric Properties of the Oblique Prism
The oblique prism displays unique slanted characteristics:
Oblique Parameters
- Bases: Parallel but shifted polygons
- Side faces: Parallelograms
- Height: Perpendicular distance between bases
- Length b: Actual edge length of parallelogram
Special Properties
- Cavalieri's principle: Same volume as right prism
- Oblique angle: Determines degree of slant
- Cross-section: Uniform throughout height
- Trigonometry: Height = b × sin(α)
Mathematical Relationships
The oblique prism follows elegant trigonometric principles:
Trigonometric Relations
Height relates to edge length via sine. Simple trigonometric relationship.
Cavalieri's Principle
Volume equals base area times height. Same as right prism formula.
Applications of the Oblique Prism
Architecture & Construction
- Slanted building facades
- Angled roof structures
- Modern architectural design
- Leaning structural elements
Engineering & Manufacturing
- Angled mechanical parts
- Sloped structural beams
- Inclined conveyor systems
- Perspective engineering
Education & Mathematics
- Cavalieri's principle demonstration
- Trigonometry applications
- 3D geometry studies
- Perspective drawing
Art & Design
- Artistic sculptures
- Perspective illustrations
- Modern furniture design
- Geometric art installations
Formula for the oblique prism
Base area (A)
Area of regular n-sided polygon base
Height (h)
Perpendicular height from oblique edge
Length (b)
Oblique edge length from height
Surface area (S)
Two bases plus n parallelogram faces
Volume (V)
Volume by Cavalieri's principle: base area times perpendicular height
Example calculation for an Oblique Prism
Given
Calculate: All properties of the pentagonal oblique prism
1. Base area calculation
The base area is 61.93 square units
2. Edge length calculation
The oblique edge length is 10.35 units
3. Volume calculation
The volume is 619.3 cubic units
4. Surface area calculation
The surface area is 423.86 square units
Summary
Complete analysis of the pentagonal oblique prism
The Oblique Prism: Where Geometry Meets Perspective
The oblique prism represents a fascinating exploration into non-perpendicular geometry, where traditional rigid vertical structures give way to slanted, dynamic forms. This geometric variation demonstrates how shifting parallel bases creates entirely new spatial relationships while maintaining fundamental volume properties. Through the elegant application of Cavalieri's principle and trigonometric relationships, the oblique prism bridges the gap between theoretical geometry and practical applications in architecture, engineering, and design.
The Beauty of Slanted Geometry
The oblique prism showcases the elegance of non-perpendicular design:
- Cavalieri's principle: Volume remains constant regardless of slant angle
- Trigonometric harmony: Height and edge length related by sine function
- Parallelogram faces: Creates dynamic visual perspective
- Architectural freedom: Enables slanted and angled designs
- Engineering flexibility: Accommodates non-vertical structural needs
- Mathematical elegance: Simple formulas with profound implications
- Design innovation: Opens new possibilities in spatial composition
Mathematical Principles and Real-World Impact
Cavalieri's Revolutionary Insight
Bonaventura Cavalieri's principle revolutionized our understanding of volume, showing that slanting doesn't change volume - a principle fundamental to the oblique prism's properties.
Trigonometric Relationships
The simple relationship h = b × sin(α) demonstrates how trigonometry governs the transition from slanted edge to vertical height, essential for practical calculations.
Architectural Innovation
Modern architecture extensively uses oblique forms to create dynamic spaces and striking visual effects, from leaning towers to angled facades.
Engineering Applications
In engineering, oblique prisms model everything from angled structural supports to inclined conveyor systems, where non-vertical orientations are essential.
Conclusion
The oblique prism stands as a testament to geometry's adaptability and practical relevance. By breaking free from perpendicular constraints, it opens doors to innovative design while maintaining mathematical rigor through Cavalieri's principle and trigonometric relationships. From the slanted walls of modern buildings to the angled components of complex machinery, oblique prisms demonstrate how mathematical concepts directly enable real-world innovations. For students and professionals alike, the oblique prism serves as an excellent example of how theoretical mathematics translates into practical applications, showing that even simple geometric variations can have profound implications for design, engineering, and our understanding of three-dimensional space. The oblique prism truly embodies the perfect fusion of mathematical principle and creative possibility.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron