Triangular Prism Calculator
Online calculator and formulas for calculating a triangular prism
Triangular Prism Calculator
The Regular Triangular Prism
A Triangular Prism has two parallel equilateral triangular faces connected by three rectangular side faces.
Triangular Prism Properties
The Classic Prism: Two parallel triangular bases with three rectangular sides
Triangular Prism Structure
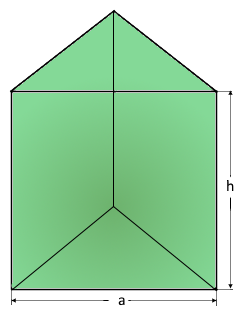
Two parallel equilateral triangular bases.
Three rectangular side faces connecting the bases.
|
|
What is a Triangular Prism?
A Regular Triangular Prism is a fundamental three-dimensional shape:
- Definition: Prism with equilateral triangular cross-section
- Bases: Two parallel congruent equilateral triangles
- Sides: Three rectangular faces connecting the bases
- Vertices: 6 corner points (3 top + 3 bottom)
- Edges: 9 edges total (6 base + 3 vertical)
- Faces: 5 faces (2 triangular + 3 rectangular)
Geometric Properties of the Triangular Prism
The Regular Triangular Prism exhibits classic prismatic properties:
Basic Properties
- Cross-section: Uniform equilateral triangle
- Parallel Bases: Identical triangular top and bottom
- Right Angles: Perpendicular side faces to bases
- Uniform Height: Constant distance between bases
Special Properties
- Convex Shape: All interior angles less than 180°
- Symmetry: 3-fold rotational symmetry about vertical axis
- Regular Base: All base edges equal length
- Simple Formula: Volume = Base Area × Height
Mathematical Relationships
The Triangular Prism follows elegant mathematical formulas:
Volume Formula
Simple multiplication of triangular base area and height. Elegant and straightforward.
Surface Formula
Sum of two triangular bases and three rectangular sides. Clear geometric composition.
Applications of the Triangular Prism
Triangular Prisms find widespread applications across many fields:
Optics & Physics
- Light refraction and dispersion
- Spectroscopy equipment
- Rainbow formation studies
- Optical instruments design
Architecture & Construction
- Roof structures and trusses
- Architectural design elements
- Structural beam analysis
- Modern building facades
Engineering & Manufacturing
- Mechanical part design
- Material volume calculations
- Packaging optimization
- Product development
Education & Research
- 3D geometry education
- Volume and area calculations
- Mathematical demonstrations
- Spatial reasoning development
Triangular Prism Formulas
Parameters
a = side length of equilateral triangular base, h = height of prism
Base Area (A)
Area of equilateral triangular base
Volume (V)
Base area multiplied by height
Height (h)
Height from volume and base side
Surface Area (S)
Two triangular bases plus three rectangular sides
Calculation Example for Triangular Prism
Given
Find: Volume and surface area of the triangular prism
1. Base Area Calculation
For a = 5:
\[A = \frac{\sqrt{3}}{4} \cdot 5^2\] \[A = \frac{\sqrt{3}}{4} \cdot 25\] \[A = \frac{25\sqrt{3}}{4} ≈ 10.83\]The triangular base area is approximately 10.83 square units
2. Volume Calculation
Using base area and height:
\[V = A \cdot h = 10.83 \cdot 140\] \[V ≈ 1516\]Or directly:
\[V = \frac{\sqrt{3}}{4} \cdot 25 \cdot 140 ≈ 1516\]The volume is approximately 1516 cubic units
3. Surface Area - Bases
Two triangular bases:
\[A_{bases} = 2 \cdot \frac{\sqrt{3}}{4} \cdot 25\] \[A_{bases} = \frac{\sqrt{3}}{2} \cdot 25\] \[A_{bases} ≈ 21.65\]Combined area of both triangular bases
4. Surface Area - Sides
Three rectangular sides:
\[A_{sides} = 3 \cdot a \cdot h\] \[A_{sides} = 3 \cdot 5 \cdot 140\] \[A_{sides} = 2100\]Combined area of three rectangular sides
5. Complete Triangular Prism
The triangular prism with perfect geometric proportions
The Triangular Prism: Foundation of Prismatic Geometry
The Regular Triangular Prism represents one of the most fundamental and versatile shapes in three-dimensional geometry. With its elegant combination of triangular bases and rectangular sides, it serves as both a practical tool in engineering and architecture and a crucial educational model for understanding prismatic principles. From the optical prisms that create rainbows to the structural elements that support our buildings, the triangular prism bridges pure mathematical beauty with real-world utility.
Properties of Regular Triangular Prisms
A regular triangular prism consists of two congruent equilateral triangles as the base and top surfaces. These are parallel to each other and their vertices are connected by three parallel edges. This creates three equally sized rectangles or parallelograms as side surfaces.
The Mathematics of Prismatic Elegance
The Triangular Prism demonstrates the beauty of geometric simplicity:
- Simple Volume Formula: Base area multiplied by height - elegant and intuitive
- Equilateral Base: All base edges equal, creating perfect triangular symmetry
- Rectangular Sides: Three congruent rectangular faces connecting the bases
- Linear Relationships: Direct proportionality between dimensions and volume
- Optical Properties: Perfect for light refraction and spectral analysis
- Structural Strength: Triangular cross-section provides excellent stability
- Mathematical Beauty: √3 appears naturally in area and volume formulas
Practical and Educational Importance
Optical Applications
Triangular prisms are essential in optics for dispersing white light into spectra, making them crucial for spectroscopy, photography, and scientific instrumentation.
Structural Engineering
The triangular cross-section provides exceptional strength-to-weight ratios, making triangular prisms ideal for roof trusses and structural frameworks.
Educational Value
As one of the simplest prisms, it serves as an excellent introduction to 3D geometry, helping students understand volume, surface area, and spatial relationships.
Design and Architecture
Modern architects frequently use triangular prismatic elements to create dynamic, geometric designs that are both aesthetically pleasing and structurally sound.
Summary
The Triangular Prism stands as a perfect example of how mathematical elegance translates into practical utility. Its simple yet powerful formulas, involving the fundamental constant √3, demonstrate the deep connections between geometry and nature. From creating rainbows through light dispersion to supporting massive architectural structures, the triangular prism proves that sometimes the most beautiful solutions are also the most practical. As students learn to calculate its volume and surface area, they're not just mastering mathematical formulas—they're discovering the geometric principles that shape our physical world, from the smallest optical instruments to the grandest architectural achievements.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron