Ramp Calculator
Online calculator and formulas for calculating a ramp
Ramp Calculator
The Ramp
A Ramp is an inclined plane with a triangular cross-section.
Ramp Properties
The inclined plane: Triangular prism with right-angled cross-section
Ramp Structure
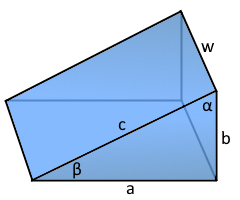
The inclined plane with triangular cross-section.
Essential for accessibility and transportation.
|
|
What is a Ramp?
A Ramp is a fundamental inclined structure:
- Definition: Inclined plane with triangular cross-section
- Right triangle: Forms 90° angle at the base
- Constant width: Uniform throughout the length
- Three sides: Base (a), height (b), hypotenuse (c)
- Slope: Gradient expressed as ratio or percentage
- Angles: α and β are complementary (sum to 90°)
Geometric Properties of Ramps
The Ramp demonstrates essential geometric principles:
Basic Parameters
- Right triangle base: 90° angle between a and b
- Hypotenuse: Inclined surface length c
- Width: Constant dimension w
- Pythagorean theorem: a² + b² = c²
Special Properties
- Accessibility: Provides gradual elevation change
- Mechanical advantage: Reduces force needed
- Slope calculation: Rise over run ratio
- Angular relationships: Complementary angles
Mathematical Relationships
The Ramp follows fundamental trigonometric principles:
Volume & Surface
Volume is half base times height times width. Surface includes all faces.
Trigonometry
Right triangle relationships for angles and sides. Slope calculated as tangent.
Applications of Ramps
Ramps are essential in numerous applications:
Accessibility & Architecture
- Wheelchair accessibility ramps
- Building entrance ramps
- Pedestrian walkways
- ADA compliance structures
Transportation & Logistics
- Loading dock ramps
- Vehicle access ramps
- Highway entrance/exit ramps
- Parking garage ramps
Engineering & Mechanics
- Inclined plane mechanics
- Conveyor systems
- Slide and chute design
- Mechanical advantage systems
Education & Safety
- Physics demonstrations
- Trigonometry applications
- Safety slope calculations
- Building code compliance
Formulas for a Ramp
Volume (V)
Volume of triangular prism
Hypotenuse (c)
Pythagorean theorem
Surface Area (S)
Total surface area
Angle (α)
Law of cosines
Side Area (AS)
Triangular face area
Top Area (AT)
Inclined face area
Slope (m)
Slope as rise over run
Ramp Parameters
Base length
Height (rise)
Hypotenuse
Constant width
All angles and sides follow right triangle relationships
Calculation Example for a Ramp
Given
Find: All properties of the ramp
1. Hypotenuse Calculation
Using Pythagorean theorem:
\[c = \sqrt{a^2 + b^2}\] \[c = \sqrt{10^2 + 4^2}\] \[c = \sqrt{100 + 16} = \sqrt{116}\] \[c ≈ 10.77\]The hypotenuse is approximately 10.77 units
2. Volume Calculation
Using the volume formula:
\[V = \frac{a \cdot b \cdot w}{2}\] \[V = \frac{10 \cdot 4 \cdot 5}{2}\] \[V = \frac{200}{2} = 100\]The volume is 100 cubic units
3. Slope Calculation
Slope as rise over run:
\[m = \frac{b}{a} = \frac{4}{10} = 0.4\]As percentage:
\[m = 0.4 \times 100\% = 40\%\]The slope is 40% or 0.4
4. Surface Area
Total surface area:
\[S = a \cdot b + w \cdot (a + b + c)\] \[S = 10 \cdot 4 + 5 \cdot (10 + 4 + 10.77)\] \[S = 40 + 5 \cdot 24.77 = 163.85\]The surface area is approximately 163.85 square units
5. Complete Ramp Properties
The ramp with practical 40% slope for accessibility
The Ramp: The Essential Inclined Plane
The Ramp represents one of humanity's most fundamental and practical geometric innovations. As an inclined plane with a triangular cross-section, the ramp bridges the gap between different elevations while providing a gradual, accessible transition. From ancient construction techniques to modern accessibility standards, the ramp embodies the perfect marriage of mathematical principles and human necessity. Its simple geometry—based on the right triangle—conceals profound applications in physics, engineering, and everyday life.
The Physics of Inclined Planes
The Ramp demonstrates fundamental physical principles:
- Mechanical advantage: Reduces force needed to lift objects
- Energy conservation: Work equals force times distance
- Friction considerations: Surface interaction affects efficiency
- Gravitational components: Forces parallel and perpendicular to surface
- Accessibility standards: Maximum slopes for safe use
- Right triangle geometry: Pythagorean relationships
- Trigonometric applications: Angles, slopes, and ratios
Engineering Excellence
Accessibility Design
Modern ramps follow strict ADA guidelines with maximum slopes of 1:12 (8.33%) for wheelchair accessibility, ensuring safe and dignified access for all users.
Transportation Systems
Highway ramps, parking structures, and loading docks rely on carefully calculated slopes to balance efficiency with safety and vehicle capabilities.
Structural Integrity
Ramp design must consider load distribution, material strength, and environmental factors while maintaining the required geometric relationships.
Mathematical Foundation
The ramp's geometry is rooted in right triangle trigonometry, providing exact calculations for all dimensions, angles, and properties.
Summary
The Ramp stands as a testament to the power of simple geometric principles applied to human needs. Its triangular cross-section, governed by the Pythagorean theorem and trigonometric relationships, provides solutions to countless practical challenges. From the ancient pyramids to modern wheelchair ramps, from loading docks to highway interchanges, the ramp continues to serve as an essential bridge between different elevations. Its beauty lies not in geometric complexity, but in the elegant simplicity with which it transforms vertical obstacles into manageable inclined paths. As both a mathematical object and a practical tool, the ramp embodies the essence of applied geometry—making the impossible accessible, one degree at a time.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron