Wedge Calculator
Online calculator and formulas for calculating a wedge
Wedge Calculator
The Wedge Shape
A Wedge is a three-dimensional shape with sloping faces and trapezoidal cross-sections.
Wedge Properties
The Sloping Shape: Trapezoidal cross-section with slanted faces
Wedge Structure
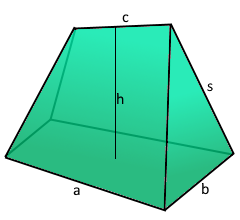
Sloping geometry with trapezoidal cross-section.
Four dimensions define the complete wedge shape.
|
|
What is a Wedge?
A Wedge is a versatile three-dimensional geometric shape:
- Definition: A shape with sloping faces and trapezoidal cross-section
- Structure: Rectangular base tapering to different top dimension
- Faces: Five faces including sloping surfaces
- Applications: Mechanical devices, construction, engineering
- Geometry: Variable cross-section along height
- Calculation: Requires four key dimensions (a, b, c, h)
Geometric Properties of the Wedge
The Wedge exhibits unique sloping geometric characteristics:
Basic Properties
- Cross-section: Trapezoidal shape varying with height
- Base: Rectangular bottom face (a × b)
- Top: Rectangular top face (c × b)
- Sloping Faces: Connect base and top edges
Special Properties
- Variable Width: Changes from base (a) to top (c)
- Sloping Edge: Diagonal connection across height
- Practical Shape: Common in mechanical applications
- Volume Formula: Uses trapezoidal area integration
Mathematical Relationships
The Wedge follows complex geometric formulas:
Volume Formula
Based on average cross-sectional area times height. Accounts for tapering geometry.
Surface Formula
Sum of rectangular base, top, and sloping faces. Involves square root calculations.
Applications of the Wedge
Wedges find widespread applications across many fields:
Mechanical Engineering
- Machine tool design
- Fastening and clamping devices
- Splitting and cutting tools
- Mechanical advantage systems
Construction & Architecture
- Foundation elements
- Structural supports
- Slope adjustments
- Architectural design elements
Manufacturing & Production
- Material forming processes
- Die and mold design
- Volume calculations for materials
- Quality control measurements
Education & Physics
- Simple machine demonstrations
- Force and motion studies
- Geometry education
- Engineering principles
Wedge Formulas
Parameters
a = base width, b = depth, c = top width, h = height
Volume (V)
Volume using trapezoidal cross-sectional integration
Surface Area (S)
Total surface area including base, top, and sloping faces
Sloping Edge (s)
Length of the diagonal sloping edge
Calculation Example for Wedge
Given Dimensions
Find: Volume, surface area, and sloping edge of the wedge
1. Volume Calculation
Using the volume formula:
\[V = b \cdot h \cdot \left(\frac{a}{3} + \frac{c}{6}\right)\] \[V = 3 \cdot 5 \cdot \left(\frac{8}{3} + \frac{6}{6}\right)\] \[V = 15 \cdot \left(\frac{8}{3} + 1\right)\] \[V = 15 \cdot \left(2.67 + 1\right) = 15 \cdot 3.67 = 55\]The volume is 55 cubic units
2. Sloping Edge Calculation
Calculate sloping edge s:
\[s = \sqrt{h^2 + \left(\frac{a-c}{2}\right)^2 + \left(\frac{b}{2}\right)^2}\] \[s = \sqrt{5^2 + \left(\frac{8-6}{2}\right)^2 + \left(\frac{3}{2}\right)^2}\] \[s = \sqrt{25 + 1^2 + 1.5^2}\] \[s = \sqrt{25 + 1 + 2.25} = \sqrt{28.25} ≈ 5.32\]The sloping edge is approximately 5.32 units
3. Surface Area Calculation
Complex surface area formula (simplified components):
Base area: a × b = 8 × 3 = 24
Top area: c × b = 6 × 3 = 18
Side areas: calculated using square root terms
\[S = a \cdot b + \text{(sloping face areas)}\] \[S ≈ 24 + 18 + \text{(complex terms)} ≈ 89.8\]The total surface area is approximately 89.8 square units
4. Complete Wedge Summary
The wedge with perfect sloping geometry for practical applications
The Wedge: Practical Geometry in Engineering
The Wedge represents one of humanity's oldest and most practical geometric forms, serving as both a fundamental simple machine and a crucial geometric shape in modern engineering. From the ancient stone wedges used to split rocks to the sophisticated mechanical components in today's precision machinery, the wedge demonstrates how geometric principles translate directly into mechanical advantage and practical utility.
The Mechanics of Sloping Geometry
The Wedge showcases the power of gradually changing cross-sections:
- Mechanical Advantage: Converts force direction and amplifies applied pressure
- Trapezoidal Cross-section: Gradually transitions from base width to top width
- Sloping Faces: Create the characteristic wedge action for splitting and fastening
- Variable Geometry: Four parameters (a, b, c, h) define complete shape
- Complex Surface Area: Requires square root calculations for sloping faces
- Volume Integration: Uses trapezoidal area formula multiplied by depth
- Practical Design: Essential for countless mechanical applications
Engineering and Practical Applications
Simple Machine Principles
As one of the six classical simple machines, the wedge converts a force applied over a longer distance into a greater force applied over a shorter distance, making it invaluable for splitting, cutting, and fastening operations.
Manufacturing Applications
Modern manufacturing relies heavily on wedge-shaped components for precision tooling, material forming, and quality control, where accurate geometric calculations are essential for proper function.
Construction and Architecture
In construction, wedges serve as essential elements for foundations, structural supports, and architectural features where sloping geometry provides both functional and aesthetic value.
Educational Value
The wedge serves as an excellent introduction to complex 3D geometry, demonstrating how mathematical formulas directly relate to physical principles and practical engineering solutions.
Summary
The Wedge stands as a perfect example of how geometric complexity serves practical purposes. Its sophisticated mathematical relationships, involving trapezoidal integration for volume and complex square root calculations for surface area, reflect the real-world complexity of the mechanical systems it enables. From the simple act of splitting wood to the precision engineering of modern manufacturing equipment, the wedge demonstrates that sometimes the most practically important shapes are also the most mathematically interesting. As students learn to calculate its volume, surface area, and sloping edge length, they're discovering the geometric principles that have been essential to human technology for millennia, while preparing for the sophisticated engineering challenges of the future.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron