Octahedron Calculator
Online calculator and formulas for calculating the properties of an octahedron
Octahedron Calculator
The Regular Octahedron
An octahedron is a platonic solid with 8 triangular faces, 6 vertices, and 12 edges.
Platonic Solid Properties
Octahedron Structure
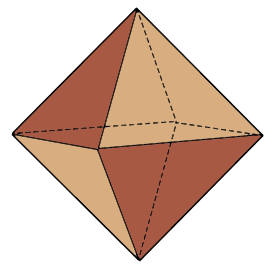
8 equilateral triangles forming a double pyramid.
|
|
Octahedron Formulas
Volume (V)
Surface Area (S)
Diagonal (d)
Dual to Cube
6 vertices ↔ 6 faces
Example Calculation
Given
Volume
Surface
Diagonal
Complete Results
About the Octahedron
The octahedron is one of the five Platonic solids, consisting of 8 equilateral triangular faces arranged in perfect symmetry. It can be visualized as two square pyramids joined at their bases, forming a double pyramid structure.
Key properties include its duality with the cube (8 faces ↔ 8 vertices), elegant formulas involving √2 and √3, and its association with the element of air in ancient Greek philosophy. The octahedron appears naturally in crystal structures, particularly in diamonds and fluorite.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron