Rhombohedron Calculator
Online calculator and formulas for calculating a rhombohedron
Rhombohedron Calculator
The Rhombohedron
A Rhombohedron is a 3D parallelogram with identical rhombic faces.
Rhombohedron Properties
The skewed cube: Six identical rhombic faces with all edges equal
Rhombohedron Structure
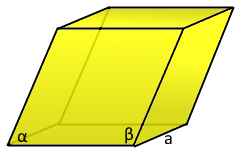
The skewed cube with rhombic faces.
All edges equal, faces are parallelograms.
|
|
What is a Rhombohedron?
A Rhombohedron is a fascinating 3D shape:
- Definition: A parallelepiped with all edges equal
- Six faces: All faces are congruent rhombi
- Equal edges: All 12 edges have the same length
- Vertices: 8 vertices total
- Angles: Two complementary angles α and β
- Symmetry: Three-fold rotational symmetry
Geometric Properties of Rhombohedrons
The Rhombohedron demonstrates remarkable geometric properties:
Basic Parameters
- Faces: 6 congruent rhombi
- Edges: 12 equal edges
- Vertices: 8 vertices
- Euler formula: V - E + F = 8 - 12 + 6 = 2
Special Properties
- Parallelepiped: Opposite faces are parallel
- Equal diagonals: Body diagonals of equal length
- Cubic deformation: Skewed cube form
- Crystal structure: Common in mineralogy
Mathematical Relationships
The Rhombohedron follows elegant mathematical principles:
Volume Formula
Uses cosine and square root functions. Accounts for angular deformation.
Surface Formula
Simple formula using sine of angle. Six times the rhombic face area.
Applications of Rhombohedrons
Rhombohedrons appear in various scientific and practical applications:
Crystallography & Mineralogy
- Calcite crystal structure
- Hematite mineral formation
- Trigonal crystal system
- Geological formations
Engineering & Design
- Architectural elements
- 3D modeling and CAD
- Mechanical components
- Structural analysis
Education & Mathematics
- Solid geometry teaching
- Trigonometry applications
- 3D visualization studies
- Mathematical demonstrations
Science & Research
- Materials science
- Crystal optics
- Lattice structures
- Molecular geometry
Rhombohedron Formulas
Volume (V)
Complex trigonometric volume formula
Surface Area (S)
Six times the rhombic face area
Complementary Angle (β)
The obtuse angle of the rhombus
Rhombic Face Area
Area of each rhombic face
Rhombohedron Parameters
a (all equal)
α (0° < α < 90°)
β = 180° - α
6 rhombi
All edges equal, faces are congruent rhombi with angles α and β
Calculation Example for a Rhombohedron
Given
Find: All properties of the rhombohedron
1. Complementary Angle
Calculate the obtuse angle:
\[\beta = 180° - \alpha\] \[\beta = 180° - 40°\] \[\beta = 140°\]The obtuse angle is 140°
2. Surface Area
Using the surface formula:
\[S = 6 \cdot a^2 \cdot \sin(\alpha)\] \[S = 6 \cdot 100 \cdot \sin(40°)\] \[S = 600 \cdot 0.643\] \[S ≈ 385.8\]The surface area is approximately 385.8 square units
3. Volume Calculation
Using the complex volume formula:
\[V = a^3 \cdot (1-\cos(\alpha)) \cdot \sqrt{1+2\cdot \cos(\alpha)}\] \[V = 1000 \cdot (1-\cos(40°)) \cdot \sqrt{1+2\cdot \cos(40°)}\] \[V = 1000 \cdot (1-0.766) \cdot \sqrt{1+2\cdot 0.766}\] \[V = 1000 \cdot 0.234 \cdot \sqrt{2.532}\] \[V = 1000 \cdot 0.234 \cdot 1.591\] \[V ≈ 372.3\]The volume is approximately 372.3 cubic units
4. Complete Rhombohedron Properties
The rhombohedron with perfect rhombic face symmetry
The Rhombohedron: The Skewed Cube
The Rhombohedron represents one of the most elegant examples of geometric deformation in three-dimensional space. Often described as a "skewed cube," this remarkable polyhedron maintains the fundamental structure of a cube while allowing for angular variation that creates a completely different geometric character. With all edges equal and all faces congruent rhombi, the rhombohedron bridges the gap between regular polyhedra and more complex geometric forms, making it both mathematically fascinating and practically important in crystallography and materials science.
The Mathematics of Deformation
The Rhombohedron demonstrates the beauty of controlled geometric deformation:
- Equal edges: All 12 edges maintain identical length
- Rhombic faces: Six congruent parallelograms with equal sides
- Angular relationships: Complementary angles α and β
- Trigonometric volume: Complex formula involving cosine and square root
- Surface simplicity: Straightforward sine-based calculation
- Crystal symmetry: Three-fold rotational axis
- Parallelepiped properties: Opposite faces parallel and equal
Crystallographic Significance
Natural Occurrence
Rhombohedrons appear frequently in nature, particularly in calcite crystals and other trigonal system minerals, demonstrating the fundamental role of this geometry in atomic arrangements.
Mathematical Elegance
The rhombohedron's formulas beautifully illustrate how simple angular changes can lead to complex trigonometric relationships in volume calculations.
Structural Properties
As a parallelepiped with equal edges, the rhombohedron combines the regularity of equal dimensions with the flexibility of variable angles.
Geometric Bridge
The rhombohedron serves as a bridge between regular cubes (α = 90°) and extremely flattened forms (α approaching 0° or 180°).
Summary
The Rhombohedron stands as a testament to the power of geometric flexibility within structural constraints. By maintaining equal edge lengths while allowing angular variation, it creates a family of shapes that spans from the familiar cube to exotic crystalline forms. Its presence in natural crystal structures demonstrates that nature itself employs this elegant geometric principle to create efficient atomic arrangements. From the mathematical perspective, the rhombohedron showcases how simple parameter changes can lead to complex trigonometric relationships, making it an excellent example of applied mathematics in both theoretical and practical contexts. Whether encountered in a geology class examining calcite crystals or in an advanced mathematics course exploring 3D geometry, the rhombohedron continues to fascinate with its perfect balance of regularity and flexibility.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron