Small Stellated Dodecahedron Calculator
Online calculator and formulas for calculating a Small Stellated Dodecahedron
Small Stellated Dodecahedron Calculator
The Small Stellated Dodecahedron
A Small Stellated Dodecahedron is a star polyhedron with pentagonal star faces and golden ratio proportions.
Small Stellated Dodecahedron Properties
The star-shaped polyhedron: 12 pentagonal star faces with golden ratio proportions
Stellated Dodecahedron Structure
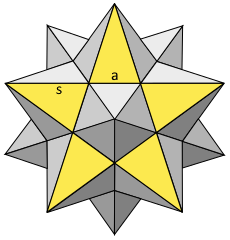
The stellated dodecahedron with pentagonal stars.
Golden ratio proportions throughout.
|
|
What is a Small Stellated Dodecahedron?
A Small Stellated Dodecahedron is one of the four Kepler-Poinsot polyhedra:
- Definition: Star polyhedron with 12 pentagonal star faces
- Stellation: Created by extending regular dodecahedron faces
- Self-intersecting: Faces penetrate through the interior
- Vertices: 12 vertices total
- Edges: 30 edges
- Golden ratio: All proportions based on φ = (1+√5)/2
Geometric Properties of Small Stellated Dodecahedrons
The Small Stellated Dodecahedron demonstrates remarkable geometric properties:
Basic Parameters
- Faces: 12 pentagonal stars (pentagrams)
- Vertices: 12 vertices (same as dodecahedron)
- Edges: 30 edges
- Euler characteristic: V - E + F = 12 - 30 + 12 = -6
Special Properties
- Self-intersecting: Non-convex star polyhedron
- Golden ratio: All proportions involve φ
- Kepler-Poinsot: One of four regular star polyhedra
- Symmetry group: Same as regular dodecahedron
Mathematical Relationships
The Small Stellated Dodecahedron follows complex golden ratio mathematics:
Volume Formula
Involves golden ratio φ and complex coefficients. Approximately 17.135 × a³.
Surface Formula
Based on pentagram areas with golden ratio. Approximately 46.165 × a².
Applications of Small Stellated Dodecahedrons
Small Stellated Dodecahedrons appear in various fields:
Art & Design
- Sculptural installations
- Architectural ornaments
- Decorative art objects
- Sacred geometry art
Mathematics & Science
- Polyhedra research
- Crystallographic models
- Golden ratio studies
- Geometric topology
Education & Research
- Advanced geometry teaching
- Symmetry group studies
- Mathematical visualization
- Kepler-Poinsot demonstrations
Spiritual & Cultural
- Sacred geometry symbols
- Meditation objects
- Esoteric studies
- Geometric mysticism
Small Stellated Dodecahedron Formulas
Edge Length (s)
Edge length using the golden ratio φ
Volume (V)
Complex volume with golden ratio terms
Surface Area (S)
Surface of 12 pentagonal stars
Circumradius (r)
Radius of circumscribed sphere
Height (h)
Height of the stellated form
Golden Ratio (φ)
The golden ratio constant
Small Stellated Dodecahedron Parameters
Pentagram side
Physical edge
12 pentagrams
φ ≈ 1.618
All dimensions are related through the golden ratio φ = (1+√5)/2
Calculation Example for Small Stellated Dodecahedron
Given
Find: All properties of the small stellated dodecahedron
1. Edge Length Calculation
Using the golden ratio formula:
\[s = \frac{a}{2} \cdot (1 + \sqrt{5})\] \[s = \frac{10}{2} \cdot (1 + 2.236)\] \[s = 5 \cdot 3.236 = 16.18\]The edge length is approximately 16.18 units
2. Volume Calculation
Using the volume formula:
\[V = \frac{5}{4} \cdot a^3 \cdot (7 + 3 \cdot \sqrt{5})\] \[V = 1.25 \cdot 1000 \cdot (7 + 6.708)\] \[V = 1250 \cdot 13.708 ≈ 17135\]The volume is approximately 17,135 cubic units
3. Surface Area Calculation
Using the surface formula:
\[S = 15 \cdot a^2 \cdot \sqrt{5 + 2 \cdot \sqrt{5}}\] \[S = 15 \cdot 100 \cdot \sqrt{5 + 4.472}\] \[S = 1500 \cdot \sqrt{9.472} ≈ 4617\]The surface area is approximately 4,617 square units
4. Circumradius
Circumscribed sphere radius:
\[r = \frac{a}{4} \cdot \sqrt{50 + 22 \cdot \sqrt{5}}\] \[r = 2.5 \cdot \sqrt{50 + 49.24}\] \[r = 2.5 \cdot \sqrt{99.24} ≈ 24.9\]The circumradius is approximately 24.9 units
5. Complete Small Stellated Dodecahedron Properties
The small stellated dodecahedron with perfect golden ratio proportions
The Small Stellated Dodecahedron: Golden Ratio in Star Form
The Small Stellated Dodecahedron stands as one of the most beautiful and mathematically profound objects in geometric art and science. As one of the four Kepler-Poinsot polyhedra—the regular star polyhedra—it represents the perfect fusion of mathematical precision and aesthetic wonder. Created by extending the faces of a regular dodecahedron into pentagonal stars (pentagrams), this extraordinary solid embodies the golden ratio in three-dimensional form. Every dimension, every angle, and every proportion is intimately connected to φ = (1+√5)/2, making it a living testament to the mathematical harmony that underlies natural beauty.
The Mathematics of Stellar Beauty
The Small Stellated Dodecahedron demonstrates the deepest geometric principles:
- Golden ratio omnipresence: Every measurement involves φ
- Pentagonal symmetry: Five-fold rotational axes
- Self-intersection: Non-convex star polyhedron
- Kepler-Poinsot membership: One of four regular star polyhedra
- Dodecahedral origin: Stellated from regular dodecahedron
- Pentagram faces: Twelve five-pointed stars
- Complex topology: Genus greater than zero
Sacred Geometry and Cultural Significance
Mathematical Legacy
Discovered by Kepler in 1619, the small stellated dodecahedron represents one of humanity's greatest geometric achievements, bridging pure mathematics and artistic expression.
Golden Ratio Beauty
Every aspect of this polyhedron reflects the golden ratio, from edge relationships to volume calculations, making it a perfect example of mathematical beauty.
Artistic Inspiration
Artists and architects have long been inspired by its star-shaped beauty, using it as a symbol of cosmic harmony and divine proportion.
Modern Applications
From crystallography to computer graphics, the small stellated dodecahedron continues to find applications in cutting-edge research and technology.
Summary
The Small Stellated Dodecahedron represents the apex of geometric beauty, where mathematical precision meets aesthetic perfection. Its twelve pentagonal star faces, all governed by the golden ratio, create a form that is both visually stunning and mathematically profound. As one of only four regular star polyhedra, it stands as a testament to the deep connections between mathematics, nature, and art. Whether studied for its complex formulas involving the golden ratio, admired for its breathtaking symmetry, or contemplated as a symbol of cosmic harmony, the small stellated dodecahedron continues to inspire mathematicians, artists, and philosophers alike. In its star-shaped faces and golden proportions, we see reflected the fundamental patterns that govern both the microscopic and cosmic scales of our universe, making it truly one of geometry's most magnificent creations.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron