Tetrahedron Calculator
Calculation of the volume and surface of an irregular tetrahedron
Irregular Tetrahedron Calculator
The Irregular Tetrahedron
An Irregular Tetrahedron is a three-dimensional shape with 4 triangular faces, 6 edges, and 4 vertices.
Irregular Tetrahedron Properties
The Simplest Polyhedron: Four triangular faces with arbitrary edge lengths
Tetrahedron Structure
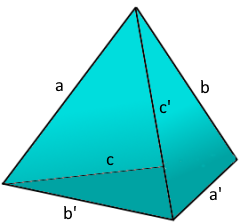
The simplest 3D polyhedron with four faces.
Six independent edge lengths define the shape.
|
|
What is an Irregular Tetrahedron?
An Irregular Tetrahedron is the most fundamental three-dimensional polyhedron:
- Definition: Simplest polyhedron with four triangular faces
- Structure: Six edges connecting four vertices
- Irregularity: All edge lengths can be different
- Faces: 4 triangular faces (not necessarily equilateral)
- Vertices: 4 corner points
- Complexity: Requires all 6 edge lengths for calculation
Geometric Properties of the Irregular Tetrahedron
The Irregular Tetrahedron exhibits unique geometric characteristics:
Basic Properties
- Faces: 4 triangular faces (any triangle type)
- Edges: 6 edges with independent lengths
- Vertices: 4 corner points in 3D space
- Euler Formula: V - E + F = 4 - 6 + 4 = 2
Special Properties
- Simplest Polyhedron: Minimum faces for 3D shape
- Flexible Geometry: Wide range of possible shapes
- No Symmetry: Generally no rotational symmetry
- Complex Calculation: Requires sophisticated formulas
Mathematical Relationships
The Irregular Tetrahedron requires complex mathematical formulas:
Volume Formula
Complex formula involving all six edge lengths. Based on determinant calculation.
Surface Formula
Sum of four triangular areas. Each calculated using Heron's formula.
Applications of the Irregular Tetrahedron
Irregular Tetrahedra find applications in various fields:
Engineering & FEA
- Finite element mesh generation
- Structural analysis elements
- Computational fluid dynamics
- 3D discretization methods
Science & Research
- Molecular geometry modeling
- Crystal defect analysis
- Biological structure studies
- Material science research
3D Graphics & Gaming
- 3D mesh primitives
- Collision detection systems
- Terrain generation
- Volume rendering
Education & Mathematics
- 3D geometry education
- Volume calculation studies
- Spatial reasoning development
- Mathematical demonstrations
Irregular Tetrahedron Formulas
Complex Mathematical Formulas
The irregular tetrahedron requires sophisticated mathematical calculations involving all six edge lengths.
Volume Formula (V)
Auxiliary calculations:
\[fa = b^2 + b'^2 + c^2 + c'^2 - a^2 - a'^2\] \[fb = a^2 + a'^2 + c^2 + c'^2 - b^2 - b'^2\] \[fc = a^2 + a'^2 + b^2 + b'^2 - c^2 - c'^2\]\[δ = a^2 \cdot b^2 \cdot c^2 + a^2 \cdot b'^2 \cdot c'^2 + a'^2 \cdot b^2 \cdot c'^2 + a'^2 \cdot b'^2 \cdot c^2\]
\[V = \frac{\sqrt{a^2 \cdot a'^2 \cdot fa + b^2 \cdot b'^2 \cdot fb + c^2 \cdot c'^2 \cdot fc - δ}}{12}\]
Based on the Cayley-Menger determinant for volume calculation
Surface Area Formula (S)
Semi-perimeters for each face:
\[p = a + b + c\] \[q = a + b' + c'\] \[r = a' + b + c'\] \[s = a' + b' + c\]Total surface area (Heron's formula for each face):
\[S = \sqrt{\frac{p}{2} \cdot \left(\frac{p}{2} - a\right) \cdot \left(\frac{p}{2} - b\right) \cdot \left(\frac{p}{2} - c\right)}\] \[+ \sqrt{\frac{q}{2} \cdot \left(\frac{q}{2} - a\right) \cdot \left(\frac{q}{2} - b'\right) \cdot \left(\frac{q}{2} - c'\right)}\] \[+ \sqrt{\frac{r}{2} \cdot \left(\frac{r}{2} - a'\right) \cdot \left(\frac{r}{2} - b\right) \cdot \left(\frac{r}{2} - c'\right)}\] \[+ \sqrt{\frac{s}{2} \cdot \left(\frac{s}{2} - a'\right) \cdot \left(\frac{s}{2} - b'\right) \cdot \left(\frac{s}{2} - c\right)}\]Sum of four triangular face areas using Heron's formula
Calculation Example for Irregular Tetrahedron
Given Edge Lengths
Find: Volume and surface area of the irregular tetrahedron
1. Auxiliary Calculations
Computing fa, fb, fc:
\[fa = 7^2 + 10^2 + 8^2 + 11^2 - 6^2 - 9^2\] \[fa = 49 + 100 + 64 + 121 - 36 - 81 = 217\]\[fb = 6^2 + 9^2 + 8^2 + 11^2 - 7^2 - 10^2\] \[fb = 36 + 81 + 64 + 121 - 49 - 100 = 153\]
\[fc = 6^2 + 9^2 + 7^2 + 10^2 - 8^2 - 11^2\] \[fc = 36 + 81 + 49 + 100 - 64 - 121 = 81\]
Intermediate values for volume calculation
2. Volume Calculation
Computing δ and final volume:
\[δ = 6^2 \cdot 7^2 \cdot 8^2 + \text{...}\] \[δ = 36 \cdot 49 \cdot 64 + \text{...} = \text{complex}\]Final calculation:
\[V = \frac{\sqrt{\text{determinant}}}{12}\] \[V ≈ 60.02\]The volume is approximately 60.02 cubic units
3. Surface Area - Face 1
Triangle with sides a, b, c:
\[p = 6 + 7 + 8 = 21\] \[s_1 = \frac{21}{2} = 10.5\] \[A_1 = \sqrt{10.5(10.5-6)(10.5-7)(10.5-8)}\] \[A_1 ≈ 20.33\]First triangular face area
4. Complete Surface Area
Sum of all four faces:
\[A_1 ≈ 20.33\] (face abc) \[A_2 ≈ 29.07\] (face ab'c') \[A_3 ≈ 35.22\] (face a'bc') \[A_4 ≈ 42.44\] (face a'b'c)\[S = A_1 + A_2 + A_3 + A_4 ≈ 127.06\]
Total surface area approximately 127.06 square units
5. Complete Irregular Tetrahedron
The irregular tetrahedron with complex geometric calculations
The Irregular Tetrahedron: Foundation of 3D Geometry
The Irregular Tetrahedron represents the most fundamental three-dimensional polyhedron, serving as the building block for understanding complex 3D geometry. With its four triangular faces, six edges, and four vertices, it embodies the minimum structure required to enclose three-dimensional space. Unlike regular tetrahedra, irregular versions allow for complete geometric freedom, making them essential tools in computational geometry, finite element analysis, and scientific modeling.
The Mathematics of Irregular Shapes
The Irregular Tetrahedron demonstrates the complexity hidden within simple structures:
- Cayley-Menger Determinant: Advanced matrix methods for volume calculation
- Six-Parameter System: Complete freedom with six independent edge lengths
- Heron's Formula Application: Surface area as sum of triangular faces
- Computational Complexity: Non-trivial calculations requiring careful implementation
- Geometric Constraints: Not all edge combinations form valid tetrahedra
- Numerical Stability: Requires robust algorithms for accurate results
- Real-World Modeling: Essential for irregular shape representation
Computational and Practical Importance
Finite Element Analysis
Irregular tetrahedra form the backbone of FEA mesh generation, allowing complex shapes to be approximated with high precision for engineering analysis and simulation.
3D Graphics and Gaming
Modern 3D engines use tetrahedral meshes for collision detection, volume rendering, and physics simulation, making irregular tetrahedra crucial for realistic graphics.
Scientific Modeling
From molecular structures to geological formations, irregular tetrahedra provide the geometric foundation for modeling natural phenomena with arbitrary complexity.
Mathematical Education
Understanding irregular tetrahedra develops spatial reasoning and introduces advanced mathematical concepts like determinants and computational geometry.
Summary
The Irregular Tetrahedron stands as a testament to the profound complexity that can emerge from seemingly simple geometric structures. As the simplest possible 3D polyhedron, it serves as the foundation for understanding more complex shapes while presenting significant mathematical challenges in its own right. The sophisticated formulas required for its analysis, involving determinants and multiple applications of Heron's formula, demonstrate how geometric irregularity introduces computational complexity. From its essential role in finite element analysis to its applications in computer graphics and scientific modeling, the irregular tetrahedron bridges pure mathematical theory with practical computational needs, making it one of the most important shapes in modern applied mathematics.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron