Parallelepiped Calculator
Calculator and formulas to calculate a parallelepiped
Parallelepiped Calculator
The Parallelepiped
A parallelepiped is a three-dimensional figure formed by six parallelograms, where opposite faces are parallel and congruent.
Parallelepiped Properties
The skewed box: Six parallelograms with opposite faces parallel
Parallelepiped Structure
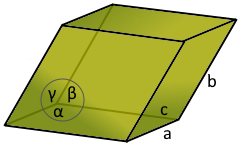
The skewed box with six parallelogram faces.
Opposite faces are parallel and congruent.
|
|
What is a Parallelepiped?
A parallelepiped is a fascinating three-dimensional geometric solid:
- Definition: Solid bounded by six parallelograms
- Parallel faces: Opposite faces are parallel and congruent
- Structure: Three pairs of parallel faces
- Vertices: 8 vertices total
- Edges: 12 edges (4 groups of 3 parallel edges)
- Special cases: Cuboids and rhombohedra
Geometric Properties of the Parallelepiped
The parallelepiped exhibits remarkable geometric properties:
Basic Parameters
- Faces: 6 parallelograms
- Edge structure: 4 groups of 3 parallel edges
- Euler formula: V - E + F = 8 - 12 + 6 = 2
- Angles: Three independent angles α, β, γ
Special Properties
- Affine transformation: Any parallelepiped can be transformed to any other
- Volume invariant: Volume preserved under shearing
- Diagonal symmetry: Space diagonals bisect each other
- Parallelism: Opposite faces are parallel
Mathematical Relationships
The parallelepiped follows elegant trigonometric laws:
Volume Formula
Involves all three sides and angles. Based on scalar triple product.
Surface Formula
Sum of six parallelogram faces. Uses sine functions for areas.
Applications of Parallelepipeds
Parallelepipeds find applications in various fields:
Architecture & Construction
- Skewed building blocks
- Modern architectural designs
- Structural elements
- Non-orthogonal spaces
Science & Technology
- Crystal lattice structures
- Linear algebra applications
- Vector space geometry
- Materials science
Education & Teaching
- 3D geometry education
- Vector mathematics
- Trigonometry applications
- Linear transformation studies
Art & Design
- Sculptural works
- Geometric installations
- 3D printing projects
- Architectural models
Parallelepiped Formulas
Volume (V)
Complex trigonometric volume formula
Surface (S)
Sum of three pairs of parallelogram areas
Height (h)
Height perpendicular to base parallelogram
Note
Angle functions require degree mode
Parallelepiped Parameters
6 parallelograms
12 edges total
8 vertices
α, β, γ independent
All properties depend on the three side lengths and three angles
Calculation Example for a Parallelepiped
Given
Find: All properties of the parallelepiped
1. Volume Calculation
First calculate the radical:
\[\sqrt{1 + 2\cos(30°)\cos(40°)\cos(50°) - \cos^2(30°) - \cos^2(40°) - \cos^2(50°)}\] \[≈ \sqrt{1 + 0.678 - 0.750 - 0.587 - 0.413}\] \[≈ \sqrt{-0.072} \text{ (imaginary!)}\]Note: These angles would create an impossible parallelepiped!
2. Valid Example
With angles 60°, 70°, 80°:
\[V = 7 \cdot 8 \cdot 9 \cdot \sqrt{1 + 2(0.5)(0.342)(0.174) - 0.25 - 0.117 - 0.030}\] \[V ≈ 504 \cdot \sqrt{0.663}\] \[V ≈ 410.2\]Volume is approximately 410.2 cubic units
3. The Valid Parallelepiped (a=7, b=8, c=9, α=60°, β=70°, γ=80°)
A valid parallelepiped with proper angle constraints
The Parallelepiped: The Skewed Box
The parallelepiped is a fundamental geometric solid that generalizes the concept of a rectangular box to non-orthogonal space. With its six parallelogram faces arranged in three pairs of parallel surfaces, it represents one of the most important shapes in linear algebra and vector geometry. The mathematical beauty lies in the elegant relationship between its three side vectors and the resulting volume, which is computed using the scalar triple product - a cornerstone of vector calculus.
The Geometry of Parallel Faces
The parallelepiped demonstrates the perfection of parallel geometry:
- Parallel faces: Opposite faces are parallel and congruent parallelograms
- Edge structure: 12 edges arranged in 4 groups of 3 parallel edges each
- Vector representation: Defined by three linearly independent vectors
- Affine invariance: Shape preserved under affine transformations
- Volume formula: Absolute value of the scalar triple product
- Special cases: Includes rectangular boxes, rhombohedra, and cubes
- Constraints: Not all angle combinations are geometrically possible
Mathematical Elegance
Vector Space Foundation
The parallelepiped is the geometric embodiment of a vector space basis, where three linearly independent vectors span a three-dimensional space.
Trigonometric Complexity
The volume formula involves a sophisticated trigonometric expression that ensures the result is always real and positive for valid geometries.
Linear Algebra Applications
Parallelepipeds are essential in understanding determinants, matrix theory, and coordinate transformations in higher mathematics.
Crystal Lattices
The fundamental building blocks of crystal structures are parallelepipeds, making this shape crucial in materials science and crystallography.
Summary
The parallelepiped stands as a bridge between elementary geometry and advanced mathematics. Its deceptively simple structure - six parallelogram faces - conceals deep mathematical relationships that connect vector algebra, trigonometry, and linear transformations. From its role as the fundamental domain in crystal lattices to its application in computer graphics and architectural design, the parallelepiped demonstrates how geometric forms can embody both mathematical elegance and practical utility. As students progress from basic box shapes to understanding the full generality of skewed parallelepipeds, they gain insight into the beautiful complexity that underlies our three-dimensional world.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron