Cuboid Calculator
Calculator and formulas for calculating the volume and surface of a cuboid
Cuboid Calculator
The Cuboid
A cuboid is a polyhedron with six rectangular faces. Opposite faces are parallel and equal.
Cuboid Properties
The rectangular box: Six rectangular faces with opposite faces parallel and equal
Cuboid Structure
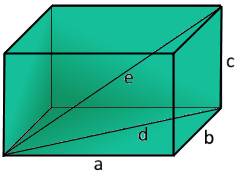
The rectangular box with three different dimensions.
Length × Width × Height.
|
|
Properties of a cuboid
A cuboid is a fundamental three-dimensional geometric shape:
- Definition: Six rectangular faces
- Opposite faces: Parallel and equal in size
- Dimensions: Length, width, and height
- Vertices: 8 corners
- Edges: 12 edges in total
- Also known as: Rectangular prism
Geometric Properties of the Cuboid
The cuboid displays fundamental geometric characteristics:
Basic Parameters
- Faces: 6 rectangles
- Edges: 12 edges (4 of each length)
- Vertices: 8 corners
- Euler Formula: V - E + F = 8 - 12 + 6 = 2
Special Properties
- Orthogonal: All angles are 90 degrees
- Parallel faces: Opposite faces are parallel
- Right angles: All edges meet at right angles
- Convex: All vertices point outward
Mathematical Relationships
The cuboid follows simple but elegant mathematical laws:
Volume Formula
Volume equals length times width times height. Straightforward and elegant.
Surface Area Formula
Surface area is twice the sum of the three face areas. Each pair of opposite faces contributes equally.
Applications of the Cuboid
Cuboids are found everywhere in our daily lives:
Architecture & Construction
- Building foundations
- Room dimensions
- Concrete blocks
- Structural elements
Packaging & Storage
- Shipping boxes
- Storage containers
- Product packaging
- Warehouse planning
Education & Learning
- Geometry lessons
- Volume calculations
- 3D visualization
- Mathematical modeling
Engineering & Manufacturing
- Machine components
- Material calculations
- CAD modeling
- Production planning
Formulas for a cuboid
Volume (V)
The volume is calculated from the product of length, width and height
Surface area (S)
The surface area is the sum of the areas of all six sides
Face diagonal (d)
The diagonal of a face using the Pythagorean theorem
Space diagonal (e)
The spatial diagonal from one corner to the opposite corner
Perimeter of base area
The perimeter of the rectangular base area
Example calculation for a cuboid
Given
Calculate: All properties of the cuboid
1. Volume calculation
The volume is 24 cubic centimeters
2. Surface area calculation
The surface area is 52 square centimeters
3. Space diagonal calculation
The space diagonal is approximately 5.39 cm
4. Perimeter of base
The perimeter of the base area is 14 cm
Summary
A complete analysis of the 4×3×2 cuboid
The Cuboid: Foundation of 3D Geometry
The cuboid is one of the most fundamental and important shapes in three-dimensional geometry. Also known as a rectangular prism or rectangular box, it forms the basis for understanding many geometric concepts. Its simple yet elegant structure, with six rectangular faces meeting at right angles, makes it an ideal starting point for exploring 3D mathematics and real-world applications.
The Beauty of Rectangular Perfection
The cuboid demonstrates the elegance of orthogonal geometry:
- Right angles: All edges meet at perfect 90-degree angles
- Parallel faces: Opposite faces are perfectly parallel and congruent
- Three dimensions: Length, width, and height define the entire shape
- Rectangular faces: All six faces are rectangles
- Symmetry: Multiple planes of symmetry
- Simplicity: Easy-to-understand formulas
- Versatility: Foundation for complex geometric constructions
Mathematical Elegance
Formula Simplicity
The formulas for cuboid calculations are beautifully straightforward, demonstrating how fundamental geometric principles can be expressed in simple mathematical terms.
Dimensional Relationships
The cuboid perfectly illustrates how changing one dimension affects volume linearly, while surface area changes in a more complex but predictable pattern.
Practical Applications
From architecture to packaging, the cuboid's practical applications are endless, making it one of the most useful geometric shapes in engineering and design.
Educational Value
As a teaching tool, the cuboid helps students understand the transition from 2D to 3D thinking, spatial relationships, and the concept of volume versus surface area.
Conclusion
The cuboid stands as a testament to the power of geometric simplicity. Its straightforward structure belies its fundamental importance in mathematics, science, and everyday life. From the boxes we ship to the rooms we live in, from the foundations of buildings to the pixels on our screens, cuboids are everywhere. Understanding the cuboid provides a solid foundation for exploring more complex three-dimensional shapes and develops spatial reasoning skills essential for mathematics, engineering, and design. As both a practical tool and a mathematical concept, the cuboid continues to be one of the most important shapes in our three-dimensional world.
|
|
|
|
Tetrahedron • Cube • Octahedron • Dodecahedron • Icosahedron